Nos exercícios a , esboce o gráfico da função, especificando o domínio, a imagem e, quando possível a paridade (par ou ímpar).
31.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos uma função e a questão pede vários comandos para a gente. Então vamos fazer cada um, não necessariamente na ordem pedida.
Começando pelo domínio, temos que lembrar que de algumas função possuem restrições:
- O denominador não pode ser zero.
- O argumento das raízes pares tem que ser maior ou igual a zero.
- O argumento da função logarítmica tem que ser maior que zero.
Como a nossa função é,
Ela não possui nenhuma restrição. Logo o domínio são todos os reais.
Agora que vimos que descobrimos o domínio, vamos partir para o gráfico.
Passo 2
Repara agora que a nossa função é o produto de um polinômio de primeiro grau com uma função modular. Então vamos ter que fazer essa multiplicação.
Mas antes de fazer as continhas vamos relembrar a definição de módulo? A definição de módulo é
Ou seja,
Podemos dar uma ajeitada e ficamos com
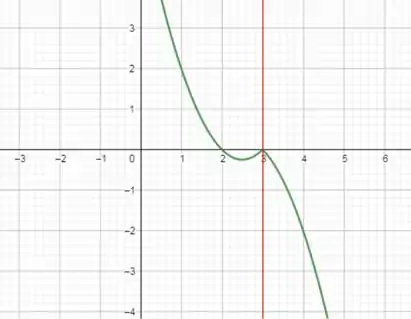
Então repara que agora a nossa função terá um comportamento para e outro comportamento para . Então vamos ter que esboçar o gráfico por partes.
Beleza?!
Passo 3
Começando por , ficamos com
Temos uma função do segundo grau, logo o gráfico é uma parabolo. Vamos então aplicar Bhaskara para descobrir as raízes,
Agora para , ficamos com
Temos uma função do segundo grau, logo o gráfico é uma parabolo. Vamos então aplicar Bhaskara para descobrir as raízes,
Note que as raízes são as mesmas. Então só temos que respeitas as concavidades para cima para a parte e para baixo para a parte . Ficará assim:
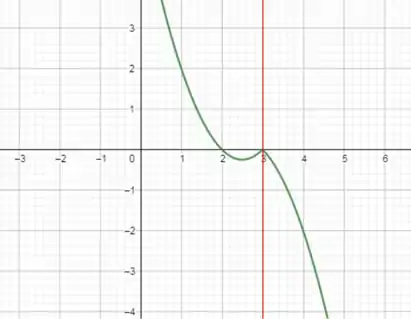
Repara também que como a nossa função vai para , a imagem também será todos os reais. Além disso, como ela não possui simetria, temos que nossa função não é par, nem impar.
Resposta