Diga se cada afirmativa abaixo é verdadeira ou falsa, justificando sua resposta:
- Uma função par com domínio real pode ser invertível, ou não invertível.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá a seguinte afirmativa:
“Uma função par com domínio real pode ser invertível, ou não invertível”
Queremos descobrir se isso é verdadeiro ou falso.
Para isso devemos analisar os conceitos de função par, além de funções invertíveis e não-invertíveis.
Passo 2
Bom... Uma função é par quando .
Isto significa que o valor assumido pela função nos pontos e são iguais.
Desta forma, podemos dizer que a função assume valores iguais para valores de simétricos.
Como exemplo, temos a função :
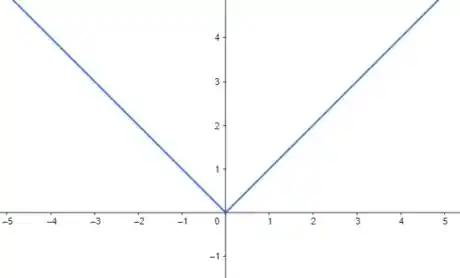
Agora queremos saber se essa função pode ser invertível ou não.
Passo 3
Bom... uma função é considerada invertível se, para cada valor no seu domínio, existe um único valor no seu contradomínio.
Assim, prosseguindo com nossa função , vemos que ela mapeia qualquer número real para o seu valor absoluto, ou seja, o valor positivo correspondente.
Vamos selecionar dois valores:
E
Observe que, neste caso, tanto quanto mapeiam para o mesmo valor absoluto, que é .
Isso significa que dois valores diferentes no domínio e estão mapeando para o mesmo valor no contradomínio , o que torna a função não injetora.
Entendeu direitinho? Responde aee ;)

Resposta
Não invertível