UFF, Cálculo IA-Lista 1, GMA, 2008-1, 32
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
Para essa função não é necessário substituir valores pra esboçar o gráfico. Quando for positivo a função terá o valor e quando for negativo a função terá o valor . Então vamos descobrir quando a função é positiva ou negativa:
Quando a função é positiva e o gráfico será uma reta horizontal que passa por . Quando a função é negativa e o gráfico será uma reta horizontal que passa por .
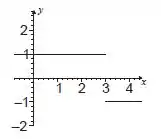Agora é só fazer o esboço, que fica assim:
Passo 2
Passo 3
Passo 4
Agora vamos especificar o domínio e a imagem. A única restrição para o domínio é quando o denominador se torna nulo. Assim, o domínio será
Quanto à imagem, pelo esboço do gráfico e as conclusões que chegamos no Passo 1, sabemos que a função só assume dois valores, e
Passo 5
Só falta verificar a paridade da função.