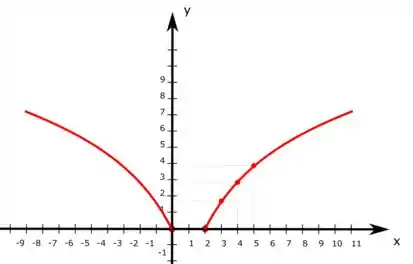
Nos exercícios 31. a 46. Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
36.
Passo 1
Opa! Para fazer o gráfico de uma função com raiz par a primeira coisa que temos que fazer é descobrir o domínio dessa função. Uma raiz par não tem solução real se o valor dentro dessa raiz é negativo, então temos que ter
Para a igualdade temos as raízes
Agora vamos ver o que acontece com valores em torno dessas raízes. Se pegarmos valores de temos
Então . Agora, para valores de entre 0 e 2, temos
O produto desses caras tem que ser negativo . Então já sabemos que não podemos ter valores de no intervalo .
Falta só ver o que acontece com essa função quando . Nesse caso temos
E aí o produto desses caras sempre vai ser positivo .
Juntando essas informações, e para garantirmos que seja raiz de números positivos, temos o seguinte domínio:
Passo 2
Agora que a gente sabe como é o domínio da nossa função vamos começar a avaliar a forma dessa função. Olha, primeiro a gente lembra da situação mais simples: uma função tem essa cara aqui
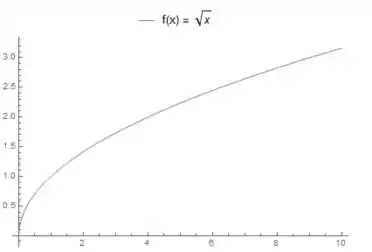
Então a gente imagina que nosso gráfico vai ter uma cara parecida com isso. A nossa diferença é que o argumento da raiz (quem está dentro da raiz) no nosso caso é a função
Ora, é uma função do segundo grau então a gente espera que tenha alguma simetria envolvida! Se olharmos o gráfico dessa parábola a gente observa o seguinte:
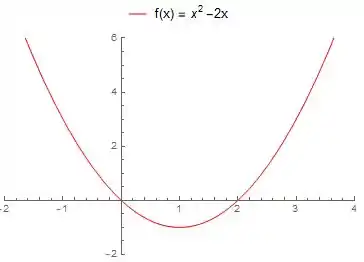
Essa parábola tem um vértice em
E sabemos que a parábola é simétrica em relação ao seu vértice. Isso quer dizer que ela é “espelhada” em relação a esse ponto. Tá! Mas o que isso tem a ver com a nossa função? Como nossa função é raiz dessa função do segundo grau que a gente acabou de estudar um pouquinho, nossa função também é simétrica em relação ao , ou seja, tudo que acontece para a gente espelha para .
Passo 3
Como encontramos o domínio da nossa função
Vamos pegar alguns valores de e marcar seus pontos no plano cartesiano. Como a gente viu que tem uma simetria em relação a , a gente só pega os valores de a partir daí e depois a gente espelha esse gráfico.Peguei os seguintes valores, lembrando que a gente só pode pegar valores de dentro do domínio:

Marcando esses pontos no plano cartesiano temos
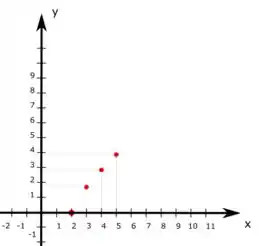
Como a gente sabe a cara de um gráfico da função raiz quadrada, desenhamos então
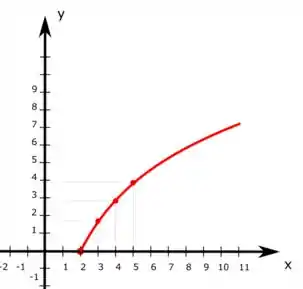
E por conta da simetria da nossa função, vamos ter a mesma figura espelhada mas partindo de . Com isso, temos
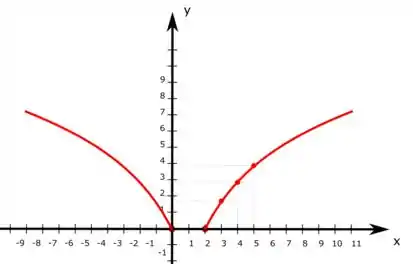
Resposta