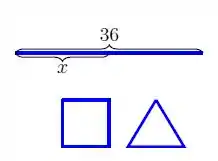
Um arame de de comprimento deve ser cortado em dois pedaços, um dos quais será dobrado para formar um quadrado e o outro, para formar um triângulo equilátero. De que modo deverá ser cortado para que a soma das áreas das regiões limitadas pelas figuras obtidas seja mínima?

No passo a gente supôs que os dois pedaços cortados são e . Beleza, agora com o pedaço nós vamos construir um quadrado de lado :

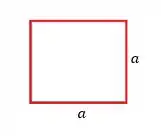
Lembra que o perímetro do quadrado é quatro vezes o lado? Então, nós temos o perímetro:

Mas o nosso pedaço tinha comprimento , então:

Isolando :

Agora com a parte do arame, nós vamos construir o triângulo equilátero. O triangulo equilátero tem todos os lados iguais, lembra?

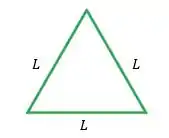
Então, o seu perímetro vai ser dado por:

Mas nós construímos o triângulo usando o pedaço de comprimento , então:

Isolando , nós temos:

Beleza, nós temos os lados e agora nós fazemos o quê? Agora nós calculamos as áreas! 😉

A área do quadrado e do triângulo equilátero são dadas pelas fórmulas:

Onde é o lado do quadrado e o lado do triângulo, tá lembrado? Beleza, então agora nós podemos somar essas áreas substituindo os valores de e que nós encontramos nos passos anteriores. Assim:

Substituindo e :

O que a gente pode fazer pra deixar tudo em função de uma variável só? Nós podemos usar a relação do passo , , pra substituir na fórmula da área:

Substituindo:

Expandindo o a potência:

Colocando em um denominador comum:

Arrumando:

Agora que colocamos tudo em função de , podemos achar a área mínima das figuras pelo gráfico dessa equação.

Percebe que a equação que nós encontramos é uma equação do segundo grau? Porque ela tem a forma: . Nesse caso, seu gráfico é dado pela parábola:

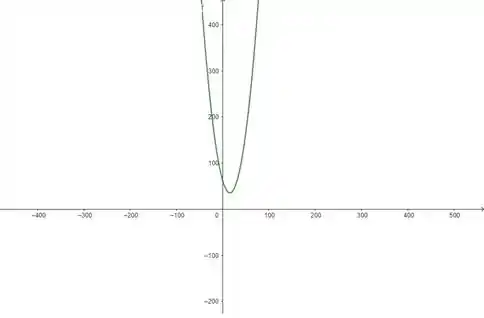
A gente não precisa saber desenhar o gráfico dessa função, apenas identificar que ele é uma parábola com a concavidade aberta para cima. E por quê? Porque o número que multiplica é positivo na função, no caso: . Se ele fosse negativo, a parábola teria concavidade para baixo.

Mas pra quê a gente tem que saber isso? Porque a questão pede que a nossa área seja mínima, e através da função a gente consegue identificar que esse ponto de mínimo acontece ali embaixo, no vértice da parábola. Só falta a gente saber o valor desse ponto.

A coordenada do vértice da parábola é dada pela fórmula:

No caso da nossa equação:

Temos e . Substituindo isso na fórmula do vértice:

Fazendo a divisão de frações e simplificando:

Achamos a coordenada do ponto de mínimo. A coordenada nós podemos encontrar substituindo o na equação dos segmentos, que nós vimos no passo :

Assim,

E temos:

Então, o nosso arame deve ser cortado em um segmento para o quadrado e para o triângulo.

É isso, galera! Encerramos o exercício! 😉