UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 3 - Taxas Relacionadas, Questão 14
14 - Um homem anda ao longo de um caminho reto a uma velocidade de . Um holofote localizado no chão a do caminho é mantido focalizado no homem. A que taxa o holofote está girando quando o homem está a do ponto do caminho mais próximo da luz?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Temos a seguinte situação nesse problema: um homem anda em linha reta a uma velocidade de e um holofote que ilumina o homem está localizado a da reta que o homem traça ao se mover.
Nessas condições queremos saber qual é a velocidade do holofote quando o homem está a de distância do ponto mais próximo ao holofote.
E agora? O que vamos fazer?? 😱
Passo 2
Primeiro vamos modelar o problema...
Se o homem anda em linha reta e o holofote está a de distância do ponto mais próximo, podemos dizer que o eixo é a trajetória do homem e em é o ponto onde o holofote se encontra. Condensando essas informações no plano ...
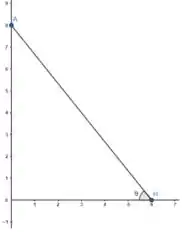
O ponto é fixo, mas o ponto varia a .
Temos que obter uma equação que relacione o ângulo com as distancias de e .
Podemos pensar que a tangente de é a razão entre o cateto oposto e o cateto adjacente, ou seja
Como é fixo, então
Aproveitando essa equação, no instante da análise do problema, o ângulo é dado quando
Tranquilo até aqui? 😁
Passo 3
Agora, se derivarmos a equação com relação a , podemos obter a taxa de variação de , veja só
Como é uma função de , para a derivada de temos que aplicar a regra da cadeia, ou seja, a derivada de dentro multiplicada pela derivada de fora...
Como a taxa de variação de é a velocidade do homem e , temos
Fim! Iae, o que achou? Responde Aí! 😁
