UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 3 - Taxas Relacionadas, Questão 12
12 - Dois lados de um triângulo têm e , e o ângulo entre eles está crescendo a uma taxa de . Encontre a taxa segundo a qual a área está crescendo quando o ângulo entre os lados de comprimento fixo for .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
O problema descreve um triangulo que tem dois lados de comprimento fixos, um de e outro de . O ângulo entre esses dois lados varia a uma taxa de e nosso objetivo é obter a taxa no qual a área está variando no momento em que o ângulo entre os lados de comprimento fixo for .
Como podemos começar esse problema? 🤔
Passo 2
Primeiramente... como podemos obter a área desse triangulo?
Pra isso, temos que descobrir qual é a altura desse triangulo, já que sabemos que a area do triangulo é dado por
Se a base for o lado fixo de , podemos definir nosso triangulo como
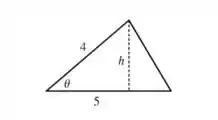
Dessa forma, a altura do triangulo pode ser obtido pela lei dos senos (o seno de um ângulo é igual a razão entre seu cateto oposto e sua hipotenusa)
Substituindo esse na fórmula da área e sabendo que é fixo como ...
Tranquilo até aqui? 😁
Passo 3
Como estamos interessados em obter a taxa de variação da área com relação ao tempo, vamos derivar ambos os lados com relação a
Como é uma função de já que está variando, para derivar temos que aplicar a regra da cadeia (a derivada de dentro multiplicada pela derivada de fora) ...
Queremos saber a variação da area quando e sabemos que a variação de é , logo
É isso! Essa resolução te ajudou? Responde Aí! ✌
