UFF, Cálculo IA-Lista 1, GMA, 2008-1, 33
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
Para esboçar o gráfico dessa função precisamos escrevê-la de uma outra forma, porque do jeito que ela está vai dar muito mais trabalho esboçar. Observe só o que acontece se fizermos a distributiva:
Uhul! Uma função do segundo grau. Ta, mas por que isso é bom? Porque já sabemos que o esboço do gráfico será uma parábola. Agora só precisamos achar as raízes e o vértice.
O vértice será:
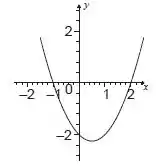
Agora podemos esboçar o gráfico.
Passo 2
Agora ver o domínio e a imagem. Como é uma função polinomial o domínio será todos os reais.
Quanto à imagem, pelo esboço do gráfico e as conclusões que chegamos no Passo 1, sabemos que:
Passo 3
Só falta verificar a paridade da função.
Resposta
Exercícios de Livros Relacionados
Encontre uma expressão para a função cujo gráfico é a curva dada:A metade superior do círculo x 2 + y - 2 2 = 4 .
Encontre uma expressão para a função cujo gráfico é a curva dada:A metade inferior da parábola x + y - 1 2 = 0 .
Encontre expressões para as funções quadráticas cujos gráficos são mostrados abaixo.
Encontre o domínio da função: h x = 1 ( x 2 - 5 x 4 )
Encontre uma fórmula para a função descrita e obtenha seu domínio.Expresse a área da superfície de um cubo como uma função de seu volume.