Uma bala é atirada de um canhão e descreve uma parábola de equação , onde é a distância e é altura atingida pela bala do canhão. Determine:
- A altura máxima atingida pela bala;
- O alcance do disparo.
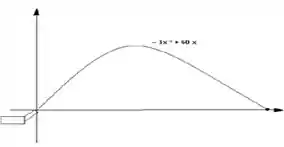
Passo 1
Repare no gráfico. A altura máxima da parábola está localizada em seu vértice, que será:
Passo 2
Olhe novamente para o gráfico. A bola saí do chão , ou seja, saí da primeira raiz. Também atinge o chão em , na segunda raiz. Dessa maneira, alcance será:
Portanto, as raízes são:
Resposta
Exercícios de Livros Relacionados
Encontre uma expressão para a função cujo gráfico é a curva dada:A metade superior do círculo x 2 + y - 2 2 = 4 .
Encontre uma expressão para a função cujo gráfico é a curva dada:A metade inferior da parábola x + y - 1 2 = 0 .
Encontre expressões para as funções quadráticas cujos gráficos são mostrados abaixo.
Encontre o domínio da função: h x = 1 ( x 2 - 5 x 4 )
Encontre uma fórmula para a função descrita e obtenha seu domínio.Expresse a área da superfície de um cubo como uma função de seu volume.