UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 3 - Taxas Relacionadas, Questão 13
13 - O topo de uma escada desliza, por uma parede vertical a uma taxa de . No momento em que a base da escada está a da parede, ela afasta-se da parede à velocidade de . Qual o comprimento da escada?
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos uma escada de comprimento que está apoiada na parede e no chão. Em um instante, a taxa de variação da altura do ponto de contato da escada e da parede é de , a taxa de variação da escada com o chão é de e a distância entra a base da escada e o chão é .
A partir daí queremos saber qual é o comprimento da escada.
Tem ideia do que fazer? 🤔
Passo 2
Se chamarmos de a distância da base da escada até a parede e a distância do chão até o topo da escada, temos
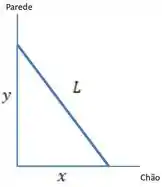
Assim o sistema parede-chão-escada forma um triangulo retângulo dado por
é um valor constante, mas e variam com o tempo, então podemos dizer que são funções do tempo.
Derivando os dois lados em relação a , temos
Assim, a derivada de é já que é uma constante e as derivadas de e devem ser obtidas pela regra da cadeia, ou seja, a derivada de dentro multiplicada pela derivada de fora.
Sabemos que a taxa de variação de é , a taxa de variação de é e quando , temos
Dessa forma, com e em mãos, substituindo em podemos obter
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
