Faça o esboço da seguinte função de grau
Passo 1
Essa questão é bem de boa né? Ele quer o esboço da função, para isso lembra quais as duas primeiras coisas a fazer? Essa é uma função de grau, então precisamos:
- Achar as raízes dessa função
- Achar a concavidade dessa função
Vamos começar com a raiz, que vai ser
Então
Assim vamos ter
Passo 2
Agora vamos para o segundo passo, que é achar a concavidade dessa função, repara que temos
Assim, como , essa função é côncava para baixo
Passo 3
Beleza, agora que sabemos essas duas informações podemos fazer o esboço do gráfico, mas antes de continuarmos vamos fazer umas contas a mais, só para deixar o nosso gráfico mais completo.
Vamos achar mais dois pontos, o extremo da parábola, e o ponto que ela corta o eixo .
O extremo, que é chamado de vértice vai ser
E
Agora vamos achar o ponto que ela corta o eixo , que vai ser quando
Assim
Passo 4
Vamos repassar as informações que achamos:
Agora é só fazer a nossa parábola
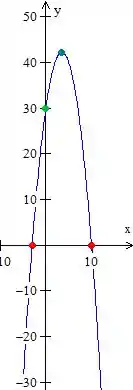
Eu marquei de diferentes cores os principais pontos que usamos só para você conseguir se localizar,
Resposta