Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução aos Vetores

Ver Teoria
Exercício 812345679101112131415161718192021222324252627282930313233343536373839404142

Enunciado

USP; Sem campus; Algebra Linear 1; P2; 2022; Questão 13

Considere um sistema de coordenadas xado em E 3 e as retas r ,   s 1 ,   s 2 e s 3 dadas pelas equações

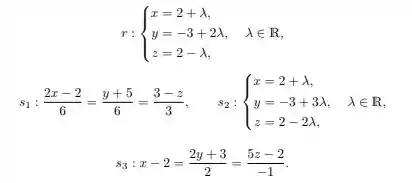
(a) r   =   s 1 ,   r   ≠   s 2   e   r   ≠ s 3

(b) r   =   s 1 ,   r   =   s 2   e   r   ≠ s 3

(c) r   =   s 1 ,   r   ≠   s 2   e   r   = s 3

(d) r     ≠   s 1 ,   r   ≠   s 2   e   r   = s 3

(e) r     ≠   s 1 ,   r   ≠   s 2   e   r   ≠ s 3

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nós queremos descobrir as relações entre as reas r ,   s 1 ,   s 2 e s 3

Para isso, vamos começar reescrevendo as nossas retas de uma forma mais familiar.

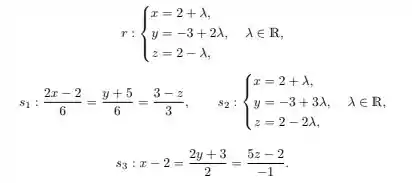
Passo 2

Vamos começar reescrevendo a reta r . Nós já temos a forma de cada ponto pertencente a reta. Temos que

( x , y , z ) ∈ r   s e

x = 2 + λ

y = - 3 + 2 λ

z = 2 - λ

Logo podemos representar a reta como:

r :   ( 2 , - 3,2 ) + λ ( 1,2 , - 1 ) ;   c o m   λ ∈ R

Vamos reescrever a reta s 1 . Nela, temos as seguintes relações

2 x - 2 6 = y + 5 6 = 3 - z 3

Logo

2 x - 2 6 = y + 5 6 = 6 - 2 z 6

Então obtemos as seguintes igualdades

2 x - 2 = y + 5

2 x - 2 = 6 - 2 z

Vamos escrever as variáveis em função de z . Então temos:

y = 2 x - 7

z = - x + 4

Logo, podemos escrever

s 1 :   ( 1 ,   2 , - 1 ) t   +   ( 0 , - 7,4 )

Passo 3

Vamos obter as outras duas retas.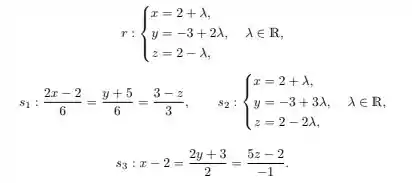

( x , y , z ) ∈ r   s e

x = 2 + λ

y = - 3 - 3 λ

z = 2 - 2 λ

Logo podemos representar a reta como:

s 2 :   ( 2 , - 3,2 ) + λ ( 1 , - 3 , - 2 ) ;   c o m   λ ∈ R

E a reta s 3

x - 2 = 2 y + 3 2 = 5 z - 2 - 1

Escrevendo as variáveis em função de z

y = - 5 z + 1 / 2

x = - 5 z + 4

Logo, podemos escrever

s 3 :   ( 4 ,   1 / 2,0 )   +   ( 5 , - 5,1 ) t

Passo 4

Agora que temos as nossas retas

r :   ( 2 , - 3,2 ) + λ ( 1,2 , - 1 ) ;   c o m   λ ∈ R

s 1 :   ( 1 ,   2 , - 1 ) t   +   ( 0 , - 7,4 )   c o m   t ∈ R

s 2 :   ( 2 , - 3,2 ) + λ ( 1 , - 3 , - 2 ) ;   c o m   λ ∈ R

s 3 :   ( 4 ,   1 / 2,0 )   +   ( 5 , - 5,1 ) t   c o m   t ∈ R

Vamos analisar seus vetores diretores. Para duas retas poderem ser iguais, elas tem que ter o mesmo vetor diretor

Logo temos que os vetores diretores de s 2 e s 3 são distintos do vetor de r . Logo   r   ≠   s 2   e   r   ≠ s 3

Mas temos que o vetor diretor de s 1 é o mesmo que o vetor diretor de r . O que precisamos verificar para que essas retas sejam iguais? Ora, elas precisam ter todos os pontos em comum. Vamos pegar um ponto qualquer de s 1 . Por exemplo o ponto ( 0 , - 7,4 ) e vamos tentar resolver a equação

( 2 , - 3,2 ) + λ ( 1,2 , - 1 ) = ( 0 , - 7,4 )

Então

λ ( 1,2 , - 1 ) = ( - 2 , - 4,2 )

Que tem solução para λ = - 2

Logo, o ponto ( 0 , - 7,4 ) pertence a s 1   e   r e como as retas são paralelas, isso implica que

r = s 1

Então, chegamos a conclusão que

  r = s 1   , r   ≠   s 2   e   r   ≠ s 3

Portanto a alternativa correta é a letra a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Prove que vec u = vec 0 harr ‖vec u‖ = 0
Prove que ‖- vec u‖ = ‖vec u‖
Prove que [(A , B) tilde (P , Q) e (C , D) tilde (P , Q)] - (A , B) tilde ( C , D ) .
Mostre que, se A≠ B , então A , B e B , A são de mesmo comprimento, mesma direção e sentido contrário.
(a) Faça um desenho ilustrando a proposição anterior no caso em que A , B , CeD são colineares.(b) Prove que ( A , B ) ~ ( C , D ) → ( B , A ) ~ ( D , C ) (c) Prove que A , B ~ C , D → C , A ~ ( D , B