USP; Sem campus; Algebra Linear 1; P2; 2022; Questão 16
Considere fixado um sistema de coordenadas , em que é uma base ortonormal de . Sabe-se que as retas
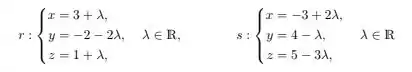
são concorrentes. Seja a reta ortogonal a e a que passa pelo ponto de interseção entre . Assinale a alternativa correspondente a um ponto que pertence a :
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Essa é bacana, vamos nessa
temos duas retas CONCORRENTES
t
mas queremos saber qual dos pontos pertencem a reta , sabendo que passa pela interseção de e é ortogonal a . Bem, vamos começar calculando a interseção das duas retas
Passo 2
queremos a interseção entre
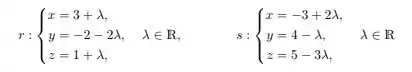
bem, a interseção é onde as coordenadas são iguais, então temos
colocando as variáveis para o mesmo lado
multiplicando a terceira equação por e somando a segunda, temos:
substituindo na segunda equação, temos que
e substituindo os dois valores na primeira equação, podemos ver que a igualdade é válida. Logo a interseção das duas retas é o ponto
Passo 3
Agora vamos obter o vetor diretor da reta . Bem para isso, precisamos dos vetores diretores das outras retas. Como
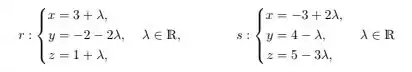
temos que
Dessa forma, como é perpendicular a essas duas retas, seu vetor diretor será perpendicular aso vetores diretores de . Que são:
Como obtemos o vetor perpendicular a esses dois? Usamos o produto veotrial. O vetor ortogonal será dado por
Passo 4
Agora que temos o vetor diretor e um ponto pertencente à reta. Podemos montar a equação da reta. Temos que
Mas queremos marca a alternativa que representa um ponto pertencente à reta. E agora?
Ora, note que fazendo , obtemos o ponto da reta
Que está presente na alternativa
portanto, a alternativa correta é a letra
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊