Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução aos Vetores

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042

Enunciado

USP; Sem campus; Algebra Linear 1; P2; 2022; Questão 15

Considere fixado um sistema de coordenadas em E 3 . Sejam r ,   s   e   t as retas

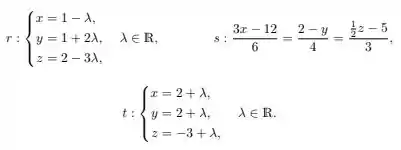
Assinale a alternativa correta:

(a) r   e   s são paralelas distintas e r   e   t são reversas

(b) r   e   s são paralelas distintas e r   e   t   são concorrentes

(c) r   =   s e r   e   t são reversas

(d) r   e   s são reversas e r   e   t são concorrentes

(e) r   e   s são reversas e r   e   t são reversas

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Queremos saber as relações entre as retas r ,   s   e   t

Bem, para isso, vamos reescrever as nossas retas de uma forma mais familiar e depois vamos analisar seus vetores diretores.

Passo 2

Como as retas são

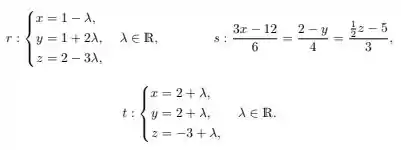
Vamos começar escrevendo r

Temos que

( x , y , z ) ∈ r   s e

x = 1 - λ

y = 1 + 2 λ

z = 2 - 3 λ

Logo podemos representar a reta como:

r :   ( 1,1 , 2 ) + λ ( - 1,2 , - 3 ) ;   c o m   λ ∈ R

Vamos reescrever a reta s . Nela, temos as seguintes relações

3 x - 12 6 = 2 - y 4 = z / 2 - 5 3

Logo

x - 4 2 = 2 - y 4 = z - 10 6

Então obtemos as seguintes igualdades

x - 4 2 = 2 - y 4

x - 4 2 = z - 10 6

Vamos escrever as variáveis em função de x . Então temos:

y = - 2 x + 10

z = 3 x - 2

Logo, podemos escrever

s :   ( 0,10 , - 2 ) + ( 1 ,   - 2,3 ) t   ;   t   ∈ R

Vamos começar escrevendo t

Temos que

( x , y , z ) ∈ r   s e

x = 2 + λ

y = 2 + λ

z = - 3 + λ

Logo podemos representar a reta como:

t :   ( 2,2 , - 3 ) + λ ( 1,1 , 1 ) ;   c o m   λ ∈ R

Passo 3

Agora que sabemos que as nossas retas são

r :   ( 1,1 , 2 ) + λ ( - 1,2 , - 3 ) ;   c o m   λ ∈ R

s :   ( 0,10 , - 2 ) + ( 1 ,   - 2,3 ) t   ;   t   ∈ R

t :   ( 2,2 , - 3 ) + λ ( 1,1 , 1 ) ;   c o m   λ ∈ R

Podemos ver que r   e   s são paralelas, mas são iguais? Para elas serem iguais basta terem um ponto em comum. Vamos ver se o ponto ( 0,10 , - 2 ) ∈ s também pertence a r . Para isso precisamos resolver o sistema

( 0,10 , - 2 ) =   ( 1,1 , 2 ) + λ ( - 1,2 , - 3 )

Logo

λ ( - 1,2 , - 3 ) = ( - 1 , - 9 , - 4 )

Que não tem solução. Logo as retas só são paralelas.

Agora, precisamos verificar se as retas r   e   t   são reversas ou concorrentes. Para verificarmos se duas retas são concorrentes basta verificarmos se elas tem pontos em comum. Ou seja se existe solução para a equação

( 2,2 , - 3 ) + t ( 1,1 , 1 ) =   ( 1,1 , 2 ) + λ ( - 1,2 , - 3 )

⇒ ( 1,1 , 1 ) t   -   λ ( - 1,2 , - 3 ) = ( - 1 , - 1,5 )

Que gera o sistema

t + λ = - 1

t - 2 λ = - 1

t + 3 λ = 5

das duas primeiras equações, obtemos que t = - 1 e λ = 0

contudo esses valores não satisfazem a terceira equação. Logo não existem t   e   λ tal que

( 2,2 , - 3 ) + t ( 1,1 , 1 ) =   ( 1,1 , 2 ) + λ ( - 1,2 , - 3 )

Dessa forma, as retas não tem interseção, logo serão reversas.

Portanto a alternativa correta é a letra a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Prove que vec u = vec 0 harr ‖vec u‖ = 0
Prove que ‖- vec u‖ = ‖vec u‖
Prove que [(A , B) tilde (P , Q) e (C , D) tilde (P , Q)] - (A , B) tilde ( C , D ) .
Mostre que, se A≠ B , então A , B e B , A são de mesmo comprimento, mesma direção e sentido contrário.
(a) Faça um desenho ilustrando a proposição anterior no caso em que A , B , CeD são colineares.(b) Prove que ( A , B ) ~ ( C , D ) → ( B , A ) ~ ( D , C ) (c) Prove que A , B ~ C , D → C , A ~ ( D , B