PSUB de Álgebra Linear 1 da USP - 2019

Em , as retas e determinam, com o plano , um tetraedro T. Então, a altura de T em relação à face contida em vale

Considere os subespaços vetoriais

Do espaço vetorial em que denota o traço da matriz A, isso é, a soma das entradas na diagonal principal de A. Então, a dimensão do subespaço vetorial é

Em , considere os subespaços vetoriais e . Então,

e

e

e

e

Considere, em , o cubo de aresta unitária e vértices A ,B, C, D, E, F, G, H, conforme a figura

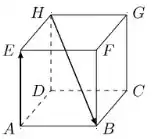
Se , então é igual a

Se é uma base de , sabemos que

Também é base de . Dado , se , então as coordenadas de em relação à base são

Em , dado um triângulo de vértices sejam pontos sobre os lados , respectivamente, tais que . Então, é igual a

Sejam , e considere, em , a reta e o plano. Se , então é igual a

Seja um espaço vetorial de dimensão e seja um subconjunto de V contendo vetores distintos. Considere as seguintes afirmações:

Se então, necessariamente,

Se é linearmente independente e , então B é base de V

Se é base de um subespaço vetorial e então B é linearmente independente.

Está correto apenas o que se afirma em

Em , as retas

São concorrentes com a reta h nos pontos A, B, e C, respectivamente. Se é o ponto médio do segmento AC, então é igual a

Seja S o subespaço vetorial de gerado por

Então, a dimensão de S é igual a

Em , seja t a reta que passa pelo ponto e é concorrente com as retas

Se é um vetor diretor de t, então é igual a

Sejam , e considere o subespaço vetorial

De . Se , então é igual a

Sejam . Então, a dimensão do subespaço vetorial do espaço vetorial é

Sejam . Sobre o sistema linear

Nas incógnitas é corretor afirmar que

, então o sistema tem exatamente uma variável livre

o sistema é compatível, para quaisquer

não existe valor de para os quais o sistema seja compatível indeterminado

se o sistema for compatível indeterminado, então

o sistema é compatível determinado se, e somente se,

Em , sejam planos cujas interseção é uma reta r. Sejam e vetores não-nulos de tais que e , e seja um vetor não-nulo paralelo a r. Considere as seguintes afirmações:

são paralelos

é uma base ortogonal de

é linearmente independente

Está correto o que se afirma em

Sabendo que, em , os pontos são os vértices de um tetraedro de volume e que os pontos e são tais que e pode-se concluir que o volume do tetraedro de vértices é igual a:

a)

b)

c)

d)

e)