Considere, em , o cubo de aresta unitária e vértices A ,B, C, D, E, F, G, H, conforme a figura
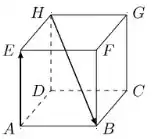
Se , então é igual a
Passo 1
Falaaa, blz?? Para começar essa questãozinha vamos notar um detalhe importante. Quando queremos projetar um vetor sobre outro, primeiro temos que colar a origem deles. Ou seja, temos que fazer a projeção olhando para os vetores da forma:
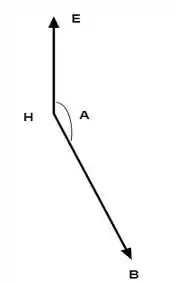
Aqui basicamente levamos o vetor até o vértice H, para colar a origem de um no outro. Agora nosso objetivo é projetar esse vetor em , vamos lembrar a fórmula para projeção?
Passo 2
Veja que no nosso caso, queremos, colocando na fórmula:
O Módulo desses vetores é mais fácil de achar, tendo em vista que é um cubo de aresta 1. Como está sobre uma aresta, temos que e a diagonal principal de um cubo, de tamanho 1 é , ou seja, .
Agora, veja que o ângulo aparente na imagem do passo 1 é , pois faz com a face superior e faz . Ou seja, já conseguimos calcular , basta acharmos o nosso vetor .
Para isso, vamos tomar os eixos da seguinte forma:
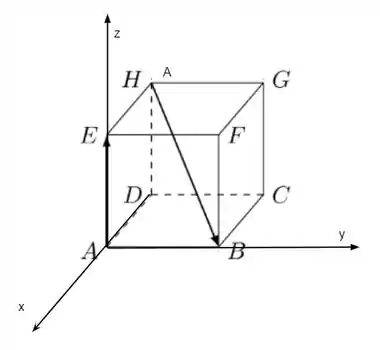
Veja que temos, nesse caso, e
Como
Passo 3
Agora, unindo tudo:
Logo:
E por isso, temos que:
E assim chegamos ao final de mais um problema, questãozinha interessante, pois faz a gente ter que pensar em alguns detalhes para nos facilitar na resolução, bora para a próxima?
Resposta
Letra A