Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Vetores

Ver Teoria
Exercício 2112345678910111213141516171819202223

Enunciado

USP, 2019, PSUB, 14

Em E 3 , dado um triângulo de vértices A , B , C , sejam P , Q , R pontos sobre os lados B C ,   C A ,   A B , respectivamente, tais que B P → =   3 P C → ,   C Q → = 3 Q A →   e   A R → = 3 R B → . Então, A P → + B Q → + C R → é igual a

a )   A B → + 2 B C →

b )   0 →

c )   2 A B → + 4 B C →

d )   A B →

e ) 1 4 A B → + 3 4 B C →

Passo 1

Falaaa, blz?? Bora começar essa questãozinha fazendo um desenho para nos ajudar

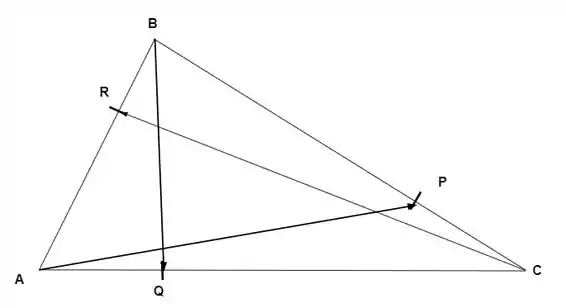
Bom, a nossa ideia aqui será escrever cada um dos vetores que queremos ( A P → + B Q → + C R → ) em função dos vetores sobre os lados, pois são as únicas informações do problema, bora lá?

Passo 2

Então bora lá, fazendo cada um deles:

A P → = A C → + C P →

B Q → =   B C → + C Q →

C R → = C B → + B R →

Agora, como queremos A P → + B Q → + C R → podemos somar as 3 equações acima e ir mexendo no lado direito, de forma esperta, vamos fazer isso:

Somando as 3:

A P → + B Q → + C R → =   A C → + C P → + B C → + C Q → + C B → + B R →

Agora a gente tem q ir mudando o lado direito para aparecer o que está nas alternativas, bora começar notando que B C → + C B → = 0 , pois é o mesmo vetor ao contrário. Deixando:

A P → + B Q → + C R → =   A C → + C P → + C Q → + B R →

Como as alternativas só possuem vetores com pontos A,B ou C se relacionando, vamos fazer o lado direito só ter isso:

C P → = 1 4 C B →

C Q → = 3 4 C A →

B R → = 1 4 B A →

Passo 3

Ficando, portanto:

A P → + B Q → + C R → =   A C → + 1 4 C B → + 3 4 C A → + 1 4 B A →

A P → + B Q → + C R → = 4 A C → + C B → + 3 C A → + B A → 4

Mas temos que 4 A C → + 3 C A → = 4 A C → - 3 A C → = A C → , ou seja:

A P → + B Q → + C R → = A C → + C B → + B A → 4

Agora aconteceu algo muito maneiro, consegue ver?

O que ocorre aqui é que A C → , C B →   e   B A → fecham um ciclo, um triangulo, ou seja A C → + C B → + B A → = 0 .

E assim finalizamos mais um probleminha interessante, bora para o próximo??

Resposta

Letra B

Exercícios de Livros Relacionados

Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.