Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Matriz que Representa uma TL

Ver Teoria
Exercício 61234578910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758

Enunciado

USP Álgebra Linear 2 P2 2016

Seja T :   M 3 x 2 →   M 3 x 2 um operador linear cujo polinômio característico é:

p T ( t )   =   t 3 ( t - 1 ) 2 ( t + 1 )

Considere as seguintes afirmações

(I) d i m ( I m g ( T ) )   ∈ { 3,4 , 5 }  

(2) T é diagonalizável se, e somente se , existirem cinco vetores distintos linearmente independentes v 1 , v 2 , v 3 , v 4 , v 5   ∈   M 3 x 2 tais que T ( v 1 )   =   v 1 , T ( v 2 )   =   v 2 e v 3 , v 4 , v 5   ∈   k e r ( T )

(3) Se A   ∈   M 6 ( R ) é uma matriz cujo polinômio característico é igual ao polinômio característico de T , então então existe uma base β de M 3 x 2 tal que [ T ] β   =   A

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez uma questão mais teórica.

Nosso objetivo é verificar a validade das afirmações, e para isso nos é informado o polinômio característico do operador T , que é dado por

p T ( t )   =   t 3 ( t - 1 ) 2 ( t + 1 )

Passo 2

Como de costume vamos começar pela primeira afirmação. Ela diz que:

d i m ( I m g ( T ) )   ∈ { 3,4 , 5 }

Será que isso é verdade? o que vocês acham? Como verificamos isso?

Bem primeiro vamos relembrar o teorema do núcleo e da imagem, lembram dele?

Ele diz o seguinte

𝐷 𝑖 𝑚 𝐼 𝑚 𝑇   +     𝐷 𝑖 𝑚 𝐾 𝑒 𝑟 𝑇   =   𝐷 𝑖 𝑚 𝑉

onde V é o espaço de origem da transformação.

Então vamos achar quem são   𝐷 𝑖 𝑚 𝐾 𝑒 𝑟 𝑇   e 𝐷 𝑖 𝑚 𝑉

Podemos usar 𝐷 𝑖 𝑚 𝑉 pelo polinômio característico, lembram que esse polinômio nos dá os autovalores da transformação e, além disso, podemos calcular os autovetores associados a esses autovalores. Se esses autovetores forem todos independentes, podemos formar uma nova BASE para o espaço.

Logo como nosso polinômio característico tem grau 6 podemos ter até 6 autovetores LI. Então

𝐷 𝑖 𝑚 𝑉   =   6

Agora para calcularmos 𝐷 𝑖 𝑚 𝐾 𝑒 𝑟 𝑇  

Um valor λ é autovalor de T se:

d e t ( T   -   λ I ) = 0

Bem, sabemos que 0 é autovalor de T , pois é raiz do polinômio característico. Pela definição de autovalor temos que:

d e t ( T   -   0 I ) = 0

d e t ( T ) = 0

mas se T tem determinante nulo, quer dizer que d i m ( k e r ( T ) )   >   0 . Além disso, como 0 é uma raiz de multiplicidade 3 podemos ter até três autovetores LI associados ao autovalor 0 , logo:

3   ≥   d i m ( k e r ( T ) )   >   0

Com isso temos que

𝐷 𝑖 𝑚 𝐼 𝑚 𝑇   +     𝐷 𝑖 𝑚 𝐾 𝑒 𝑟 𝑇   =   𝐷 𝑖 𝑚 𝑉

𝐷 𝑖 𝑚 𝐼 𝑚 𝑇   =   𝐷 𝑖 𝑚 𝑉   -     𝐷 𝑖 𝑚 𝐾 𝑒 𝑟 𝑇  

⇒ 𝐷 𝑖 𝑚 𝐼 𝑚 𝑇   ∈   { 3,4 , 5 }

Passo 3

No passo anterior vimos que a primeira afirmação é verdadeira, vamos para a segunda afirmação. Ela diz que:

T é diagonalizável se, e somente se , existirem cinco vetores distintos linearmente independentes v 1 , v 2 , v 3 , v 4 , v 5   ∈   M 3 x 2 tais que T ( v 1 )   =   v 1 , T ( v 2 )   =   v 2 e v 3 , v 4 , v 5   ∈   k e r ( T )

Lembram a definição de matriz diagonalizável? Vamos relembrar!!!

Dizemos que 𝐴   é diagonalizável se pode ser escrita da seguinte forma:

𝐴   =   𝑃 𝐷 𝑃 − 1

Com 𝐷   uma matriz diagonal onde suas entradas são os autovalores de 𝐴   , e 𝑃   a matriz onde suas colunas são os autovetores de 𝐴   . Além disso, para A ser diagonalizável, o número de vetores LI associados a cada valor precisa ser igual a multiplicidade algébrica daquele autovalor, isto é:

Se λ for raiz do polinômio característico e tem multiplicidade algébrica k , então a matriz só será diagonalizável se existirem k vetores LI associados ao autovalor λ .

Ao revisarmos a condição para ser diagonalizável, percebemos que a afirmação 2 satisfaz essas condições. Logo ela é verdadeira.

Passo 4

Para finalizar, vamos verificar a última afirmação. Ela diz o seguinte:

Se A   ∈   M 6 ( R ) é uma matriz cujo polinômio característico é igual ao polinômio característico de T , então então existe uma base β de M 3 x 2 tal que [ T ] β   =   A

E aí, será que essa afirmação é verdadeira? O que vocês acham?

Bem essa questão está dizendo que qualquer que seja a matriz A , se ela tiver o mesmo polinômio característico de T então existe uma base β de M 3 x 2 tal que [ T ] β   =   A . Vamos dar um contra exemplo para essa afirmação Suponha que A e [ T ] c a n sejam as matrizes abaixo:

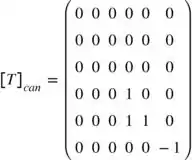
Claramente, ambas têm o mesmo polinômio característico, mas como [ T ] c a n não vai ser diagonalizável, então não existe uma base M 3 x 2 tal que [ T ] β   =   A .

Logo a afirmação 3) é falsa

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

d)

Exercícios de Livros Relacionados

Seja T o operador linear dado pela matriz: 1 2 - 1 2 0 1 1 - 2 2 a) Calcular N ( T ) e dim ⁡ N ( T ) . b) Calcular I m ( T ) e dim ⁡ I m ( T ) .
Seja o espaço vetorial V = M ( 2 ,2 ) e a transformação linear T : V → R 3 , T a b c d = ( a + b , c - d , 2 a ) a) Mostrar que T é linear.b) Determinar T B A sendo A e B as bases canônicas de M ( 2 ,
Consideremos as transformações lineares S e T de R 3 em R 2 definidas por S x , y , z = ( 2 x - y , 3 x - 2 y + z ) e T x , y , z = ( x + y - z , y - 2 z ) .a) Determinar o núcleo da transformação lin
As transformações S :R 2 → R 3 e T :R 3 → R 2 são tais que S x , y = ( y , x - y , 2 x + 2 y ) e T x , y , z = ( x , y ) .a) Sendo B = { 1 ,0 , - 1 ,1 ,1 ,1 ,1 ,0 ,0 } uma base do R 3 , determinar a m
Sendo S e T operadores lineares do R 3 definidos por S x , y , z = ( x ,2 y , x - y ) e T x , y , z = ( x - z , y , z ) , determinar:a) [ S ∘ T ] .b) [ T ∘ S ] .