Sejam e e considere as seguintes afirmações:
- Se e são semelhantes, então qualquer autovalor de é autovalor de
- Se e são operadores lineares uma base de , e e se e são semelhantes então todo autovetor de também é autovetor de .
- Se e possuem os mesmos autovalores com as mesmas multiplicidades algébricas, então e são semelhantes.
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Algelin, dessa vez uma questão teórica.

Nosso objetivo nessa questão é verificar quais afirmações são verdadeiras. Então vamos lá!!!
Passo 2
Vamos começar pela afirmação mais fácil, a 3. Ela diz o seguinte:
Se e possuem os mesmos autovalores com as mesmas multiplicidades algébricas, então e são semelhantes.
Segundo ela, temos duas matrizes quadradas , e . Daí, se essas matrizes possuírem os mesmos autovalores e com as mesmas multiplicidades algébricas, podemos afirmar que elas são semelhantes? É isso que vamos verificar...
E aí, vocês acham que é verdade? Como podemos verificar essa afirmação?
Bem, primeiro, vamos revisar a definição de matrizes semelhantes.
Uma matriz é dita semelhante a uma matriz se existe uma matriz tal que:
Essa definição parece com a definição de matriz diagonalizável, né?

Suponha que seja da forma:

e matriz nula.
Ambas as matrizes tem o polinômio característico dado por:
Mas essas matrizes não são semelhantes, pois não é diagonalizável enquanto que
é uma matriz diagonal.
Logo a afirmação 3 é falsa.
Passo 3
Agora vamos checar a primeira afirmação: Ela diz que se e são semelhantes, então qualquer autovalor de é autovalor de . Será que é verdade? Vamos provar!!!
Para isso, precisamos mostrar que os polinômios característicos de duas matrizes semelhantes são iguais. Como o polinômio característico de uma matriz é dado por
temos:
(como e são semelhantes)
então:
(usando o fato que )
(multiplicando)
(pela semelhança)
Ou seja, os polinômios característicos de duas matrizes semelhantes são iguais. Logo a primeira afirmação é verdadeira

Passo 4
Para finalizar a questão, vamos verificar a afirmação 2. Ela diz o seguinte:
Se e são operadores lineares e uma base de , e e se e são semelhantes então todo autovetor de também é autovetor de .
Vamos dar um contra exemplo para essa afirmação.
Sejam e as seguintes matrizes
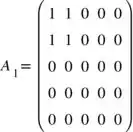
e são semelhantes ( é a diagonalização de ), Mas o vetor é autovetor de e não de .

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
1)