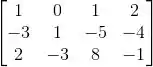P1 de Álgebra Linear da UFRJ - 2018.2

A é uma matriz qualquer. Escalonando-se A, aparece uma linha de zeros. Considere as afirmações abaixo:

(I) Pode-se concluir que o conjunto das colunas de A é linearmente dependente.

(II) Pode-se concluir que o conjunto das linhas de A é linearmente dependente.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

O sistema linear associado à matriz aumentada:

Tem solução única Então é:

(a) 8

(b) 18

(c) 22

(d) 26

Seja A uma matriz Aplicando-se operações elementares às linhas de A, obtém-se a matriz E abaixo:

Pode-se afirmar que:

(a) é base do espaço gerado pelas linhas de A.

(b) gera a imagem de A.

(c)

(d)

O sistema

Admite solução(ões) se e somente se:

(a)

(b)

(c)

(d)

Qual dos vetores abaixo pode ser acrescentado ao conjunto para se obter uma base do núcleo da matriz ?

(a) Nenhum vetor, já é base.

(b) (2,1,0,1)

(c) (1,0,1,0)

(d) (1,2,1,0)

A dimensão da imagem de

É:

(a) 0

(b) 1

(c) 2

(d) 3

Sejam uma base de e um vetor não nulo. Considere as afirmações abaixo:

(I) Se pertence aos planos e , então pertence à reta

(II) Os subespaços e se interceptam em apenas um ponto.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Os vetores , e do são as colunas da matriz aumentada de um sistema linear:

Considere as seguintes situações distintas:

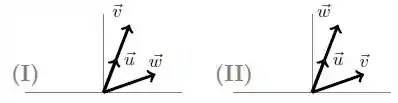
(a) O sistema (I) tem solução única.

(b) O sistema (I) tem infinitas soluções.

(c) O sistema (II) tem solução única.

(d) O sistema (II) tem infinitas soluções.

Os núcleos das matrizes

são dois planos de . A interseção destes planos é:

(a) o conjunto vazio.

(b) um ponto.

(c) uma reta.

(d) um plano.

Considere as afirmações abaixo:

(I) é gerador de

(II) é uma base de

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Qual é a solução geral do sistema abaixo?

Obs: abaixo, s e t são parâmetros reais.

(a)

(b)

(c)

(d)

Considere o sistema S representado pela matriz aumentada

onde é um conjunto linearmente independente. Assinale a matriz aumentada que representa um sistema equivalente a S.

(a)

(b)

(c)

(d)

Com relação ao sistema linear com , considere as afirmações abaixo:

(I) Se e são soluções de S, então é solução de

(II) Se S não admite solução, então não admite solução.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja A uma matriz tal que:

e:

Então vale:

(a)

(b)

(c)

(d)

Sejam , e sequências infinitas definidas por , e . Considere a soma e o produto por escalar análogos aos do (isto é, componente a componente). Então a é:

(a) 1

(b) 2

(c) 3

(d) Infinito