O sistema linear associado à matriz aumentada:
Tem solução única Então é:
(a) 8
(b) 18
(c) 22
(d) 26
Passo 1
Vamos aproveitar que a questão deu a matriz na forma aumentada e escalonar ela:
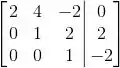
Passo 2
Agora fica mais fácil de achar a solução!
Pela terceira linha:
Substituindo na equação dada pela segunda linha:
Substituindo agora e na equação da primeira linha:
E a solução única vai ser então:
Fazendo a continha que foi pedida no enunciado:
Resposta
(c) 22
Exercícios de Livros Relacionados
Para cada sistema do Exercício 3 que for linear, determine se é consistente.
Em cada parte, determine se as equações formam um sistema linear no sistema: - 2 x + 4 y + z = 2 3 x - 2 y = 0
Na linha do exercício anterior, mostre que se a1b2 − a2b1 ≠ 0 então o sistema admite sempre uma solução do tipo (x, y, 0).
No sistema abaixo, atribua sucessivamente valores aos parâmetros m, n de modo que as três equações representem um único plano, dois planos ou três planos: x-2 y-3 z=m3 x-6 y-9 z=n- 2 x+4 y+6 z=1
Para cada um dos sistemas abaixo, decida em qual dos casos (primeiro a oitavo) discutidos no texto ele se enquadra. Determine também todas as soluções do sistema, se houver. 3 x-5 y+2 z=14 x-3 y+z=22