Os vetores , e do são as colunas da matriz aumentada de um sistema linear:
![]()
Considere as seguintes situações distintas:
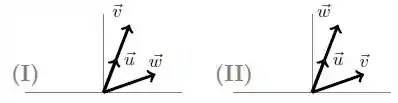
(a) O sistema (I) tem solução única.
(b) O sistema (I) tem infinitas soluções.
(c) O sistema (II) tem solução única.
(d) O sistema (II) tem infinitas soluções.
Passo 1
Quando temos uma matriz aumentada da forma:
![]()
onde , e são vetores das colunas, as nossas soluções são os vetores do tais que:
Passo 2
Se olhamos pra situação (I), o sistema dado nunca vai ter solução, pois não existirão valores de x e y satisfazendo
Isso ocorre porque , estão em uma mesma direção, e ao fazer CLs desses dois caras eu só vou obter vetores que também estão naquela direção: nunca vamos conseguir obter o vetor mostrado na figura!
Com isso já eliminamos os itens (a) e (b).
Passo 3
Agora vamos ver a situação (II).
Como o vetor está na direção do vetor , ele é um múltiplo escalar desse vetor.
Se pensarmos no sistema linear dado e na nossa relação que desenvolvemos no Passo 1:
Vamos ter que x é um escalar específico e y vale 0.
Assim, vai existir um só vetor solução , e o sistema tem solução única.
Essa resposta está no item (c).
Resposta
(c) O sistema (II) tem solução única.