A dimensão da imagem de
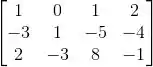
É:
(a) 0
(b) 1
(c) 2
(d) 3
Passo 1
Como queremos saber a dimensão da imagem (que é o espaço gerado pelas colunas), podemos apenas escalonar essa matriz.
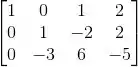
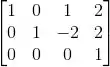
Nenhuma linha zerou, então:
Como:
Temos:
Resposta
(d) 3
A dimensão da imagem de
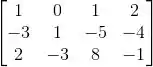
É:
(a) 0
(b) 1
(c) 2
(d) 3
Como queremos saber a dimensão da imagem (que é o espaço gerado pelas colunas), podemos apenas escalonar essa matriz.
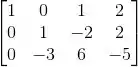
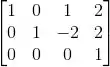
Nenhuma linha zerou, então:
Como:
Temos:
(d) 3