P4 de Álgebra Linear da UFRJ - 2017.2

Considere o sistema linear onde é uma matriz quadrada que não possui autovetores:

sempre admite solução.

Quando admite solução, ela não é única.

(a) é falsa e é verdadeira

(b)Ambas são falsas

(c) Ambas são verdadeiras

(d) é verdadeira e é falsa

Qual das matrizes abaixo pode não ser simétrica?

(a)

(b)

(c)

(d)

Considere o paralelepípedo em abaixo,

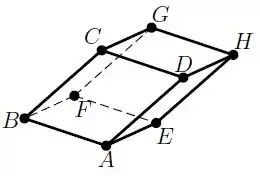
onde , , e . O volume deste paralelepípedo é:

(a)

(b)

(c)

(d)

Considere as afirmativas abaixo:

I - Se é uma matriz injetiva, então .

II - Se é uma matriz sobrejetiva, então .

(a) é falsa e é verdadeira.

(b) é verdadeira e é falsa.

(c) Ambas são verdadeiras.

(d) Ambas são verdadeiras.

Seja o plano gerado pelos vetores e . O vetor de que está o mais próximo possível do vetor é:

(a)

(b)

(c)

(d)

Calcule o determinante da matriz :

(a)

(b)

(c)

(d)

Sejam e subespaços vetoriais de , com e. Qual opção abaixo não pode acontecer?

(a)

(b)

(c)

(d)

Sejam , , e números quaisquer. O sistema:

nunca tem solução

sempre tem várias soluções

só tem solução se

só tem solução se

Assinale a soma dos módulos das componentes de um autovetor unitário associado ao menor autovalor da matriz:

É dado que o conjunto dos autovalores da matriz é Então:

(a) não é diagonalizável

(b) é uma reflexão ortogonal

(c) é uma reflexão não ortogonal

(d) é uma projeção

Seja uma transformação linear tal que e Seja matriz de na base canônica. Calcule a soma dos elementos da primeira linha de

(a)

(b)

(c)

(d)

Calcule as coordenadas de na base

(a)

(b)

(c)

(d)

Sejam e duas bases de . A matriz de mudança de base de para é igual a:

(a)

(b)

(c)

(d)

Suponha que a matriz tem dois autovalores distintos, e , e que e são autovetores associados ao autovalores . Quais dos vetores abaixo poderia ser um autovetor associado a

(a)

(b)

(c)

(d)

Seja tal que e . As entradas da diagonal de , e , são:

(a) e

(b) e

(c) e

(d) e

Assinale a alternativa correta com relação à matriz:

(a) não tem inversa, nem é diagonalizável.

(b) é inversível e diagonalizável.

(c) é inversível, mas não é simétrica.

(d) não tem inversa, mas é diagonalizável.