Assinale a alternativa correta com relação à matriz:

(a) não tem inversa, nem é diagonalizável.

(b) é inversível e diagonalizável.

(c) é inversível, mas não é simétrica.

(d) não tem inversa, mas é diagonalizável.

Para ter inversa, a matriz precisa ter o determinante diferente de 0 o que acontece quando as linhas e colunas formam conjuntos de vetores

Mas olhando para a matriz, vamos que as duas últimas colunas são múltiplas uma da outra, o que torna o conjunto das colunas Isso basta para que o determinante seja 0 e a matriz não seja inversível. Resta descobrirmos se ela é ou não diagonalizável!

E vou te contar um segredo muuuuuito legal agora! Ta vendo que essa matriz pode ser quebrada em blocos?

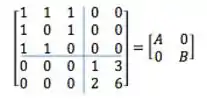
Sendo:

Quando isso acontece, se cada um dos blocos for diagonalizável, a matriz cheia também vai ser! Irado né?

A matriz é simétrica! Então pelo teorema espectral, ela é diagonalizável! Show, vamos ver a agora!

Como a matriz tem 2 autovalores distintos, ela vai ser diagonalizável!

Então, como e são diagonalizáveis,