Sejam e subespaços vetoriais de , com e. Qual opção abaixo não pode acontecer?
(a)
(b)
(c)
(d)
Passo 1
Primeiramente vamos deixar bem definido na nossa cabeça que soma é diferente de união!
Quando somamos dois subespaços, pegamos todos os elementos de um deles e somamos com todos os elementos do outro. Assim, a soma poderia resultar o
Mas na união não somamos cada elemento de cada subespaço, apenas juntamos os espaços.
Passo 2
Então por exemplo, se for uma reta em e também for uma reta em vamos ter o seguinte como
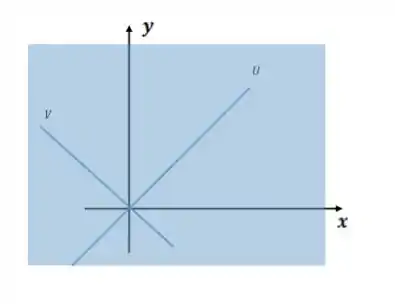
A soma dos subespaços nesse caso vai ser o espaço que obtemos juntando a base de com a base de V, no caso vai ser o próprio .
Mas a união vai ficar assim:
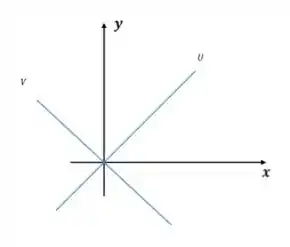
E duas retas separadas assim, nunca vai ser um subespaço vetorial, muito menos o .
Assim conseguimos provar que a letra d) é a alternativa impossível de acontecer.
Resposta
d