P4 de Álgebra Linear da UFRJ - 2018.2

Seja A uma matriz cujas colunas geram um espaço de dimensão 3. A dimensão do núcleo de A é:

(a) 2

(b) 3

(c) 4

(d) 5

Seja

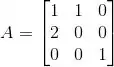
Os autovetores de A associado ao autovalor 2 são da forma:

(a)

(b)

(c)

(d)

Sejam A e B matrizes quadradas Considere as afirmações abaixo:

(I) Se A e B são invertíveis, então AB é invertível.

(II) Se AB é invertível, então A e B são invertíveis.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja a rotação de 90° no sentido horário em torno da origem seguida pela projeção ortogonal sobre o eixo x. Calcule a matriz de T (em relação à base canônica).

(a)

(b)

(c)

(d)

Calcule a reflexão ortogonal do vetor através do plano gerado por e

(a) (1,0,-1,1)

(b) (0,0,-1,0)

(c) (0,0,-1,1)

(d) (0,1,-1,0)

Seja A uma matriz Considere as afirmações abaixo:

(I) Se as colunas de U formam uma base do composta por autovetores de A então existe D diagonal tal que

(II) As matrizes e tem os mesmos autovalores.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Considere as afirmações abaixo:

(I) Seja uma combinação linear de vetores do com coeficientes todos não nulos. Então cada vetor é combinação linear dos demais vetores do conjunto

(II) Seja A uma matriz na forma escalonada. Então uma coluna que não contém pivô é combinação linear das colunas a sua esquerda.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Considere as afirmações abaixo:

(I) é uma base de

(II) é gerador de

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Considere as afirmações abaixo:

(I) Considere um sistema linear que não admite solução e seja a matriz aumentada desse sistema. Então

(II) Se o sistema tem solução única, então A é injetiva.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja uma matriz cujas colunas são os vetores e . Suponha que O determinante da matriz vale:

(a) 15

(b) 16

(c) 18

(d) 19

Calcule os autovalores da matriz:

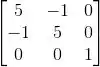
(a) 1, 2 e 6.

(b) 1, 3 e 7.

(c) 1, 4 e 6.

(d) 1, 3 e 5.

Sejam e então:

(a)

(b)

(c)

(d)

Encontre o modelo quadrático da forma que melhor se ajusta (no sentido dos mínimos quadrados) aos dados experimentais da tabela abaixo. Assinale o valor do coeficiente b.

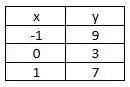
(a) 2

(b) 3

(c) 4

(d) 5

Seja u um autovetor unitário da matriz simétrica A, relativo ao autovalor Seja a forma quadrática associada a A. Assinale o valor de

(a)

(b)

(c)

(d)

Seja A uma matriz injetiva. Sejam e soluções dos sistemas e respectivamente. A solução de

(a)

(b)

(c)

(d)

Sejam e duas matrizes, respectivamente, e . Pode-se afirmar que:

(a)

(b)

(c)

(d)