Considere as afirmações abaixo:
(I) é uma base de
(II) é gerador de
(a) (I) é falsa e (II) é falsa.
(b) (I) é falsa e (II) é verdadeira.
(c) (I) é verdadeira e (II) é falsa.
(d) (I) é verdadeira e (II) é verdadeira.
Passo 1
(I) Pra um conjunto ser base, ele tem que ser capaz de gerar todo o espaço e ser linearmente independente.
Como temos 3 vetores do , vamos ver se esses três vetores são LI.
Pra isso, vamos coloca-los nas linhas de uma matriz e escalonar:

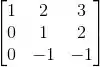

Como nenhuma linha zerou, os três vetores são linearmente independentes, logo formam uma base para
Passo 2
(II) Pra esse conjunto com 3 vetores ser gerador de , ele vai ter que ser capaz de gerar todo o
Por isso, os vetores vão ter que ser LI.
Vamos ver se isso é verdade colocando-os nas linhas de uma matriz e escalonando:



A última linha zerou, logo ela é combinação linear das duas linhas anteriores a ela.
Então o espaço gerado por aqueles 3 vetores é
E com dois vetores de não conseguimos gerar todo esse espaço.
Portanto a afirmação II é falsa, e o conjunto dado não é gerador de
Resposta
(c) (I) é verdadeira e (II) é falsa.