Sejam e duas matrizes, respectivamente, e . Pode-se afirmar que:
(a)
(b)
(c)
(d)
Passo 1
Vamos analisar alternativa por alternativa.
(a)
Não podemos afirmar isso, pois A é e é
Para que essa regra do produto seja válida, as duas matrizes têm que ser quadradas e de mesma ordem.
Passo 2
Antes de analisar as próximas alternativas, vamos lembrar de umas coisas.
Primeiro, a matriz A é uma matriz Então ela tem nas linhas vetores do .
Se temos 4 vetores do , então com certeza um deles pelo menos é combinação linear dos demais.
Logo, A tem linhas LD e:
Agora, B é uma matriz então suas colunas são vetores do .
E acontece a mesma coisa: temos 4 vetores do então com certeza um deles é combinação linear dos demais, pelo menos.
Portanto:
Beleza, agora vamos continuar vendo as alternativas.
Passo 3
(b)
Primeiro vamos chamar o produto de uma nova matriz .
Sabemos pela regra de multiplicação de matrizes, que a matriz C vai ser
Além disso, ela vai ser uma combinação linear das colunas de A, com coeficientes dados pelas entradas das colunas de B, desse jeito aqui ó:
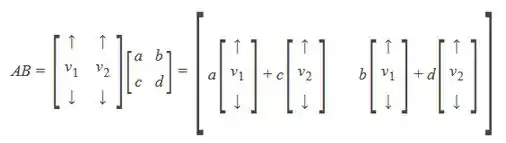
Mas vimos que as colunas de B são LD, certo?
Então com certeza as colunas de também vão ser LD.
Aí então:
E essa afirmativa é verdadeira e é a resposta.
Vamos ver por que as outras estão erradas.
Passo 4
(c)
Primeiro vamos chamar o produto de uma nova matriz .
Sabemos pela regra de multiplicação de matrizes, que a matriz D vai ser
Além disso, ela vai ser uma combinação linear das colunas de B, com coeficientes dados pelas entradas das colunas de A, do mesmo jeito que vimos antes no passo 3.
Mas agora não vai ter problema algum, porque as colunas de A não são necessariamente LD.
Então não necessariamente vamos ter:
Somente se as colunas de A forem LD.
Passo 5
(d)
Vimos no Passo 3 que necessariamente:
E depois vimos no Passo 4 que não necessariamente também temos
Então essas duas coisas podem não ser iguais, por isso a letra (d) não pode ser a resposa.
Resposta
(b)