Seja
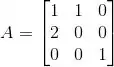
Os autovetores de A associado ao autovalor 2 são da forma:
(a)
(b)
(c)
(d)
Passo 1
Para acharmos os autovetores associados a um dado autovalor , resolvemos o sistema homogêneo:
Fazendo isso para e a matriz A dada, ficamos com o sistema:
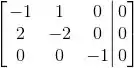
Pela terceira equação:
Usando a primeira ou segunda equação:
Então os autovetores são da forma:
E , pois se não teremos um vetor nulo, que não pode ser autovetor.
Por isso a resposta é a letra (d).
Resposta
(d)