Calcule os autovalores da matriz:
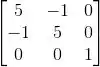
(a) 1, 2 e 6.
(b) 1, 3 e 7.
(c) 1, 4 e 6.
(d) 1, 3 e 5.
Passo 1
Pra calcular autovalores de uma matriz A, fazemos:
Fazendo essa conta para a matriz dada:
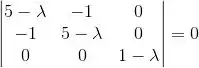
Temos então duas possibilidades:
Ou:
Temos então os autovalores 1, 4 e 6.
Resposta
(c) 1, 4 e 6.
Exercícios de Livros Relacionados
Determinar valores próprios do operador linear T : V → V do R 4 que é definido em uma base { e 1 ,..., e n } por T e i = λ i ∈ R .
Achar os valores e os vetores próprios do operador T do IR 2 dado por:T(x, y) = (x + y, x - y);
Calcular o polinômio característico e os valores próprios da matriz: 2 1 0 0 0 2 0 0 0 0 1 1 0 0 - 2 4
Seja 1 1 0 1 a matriz de um operador do R 2 . Ache os valores próprios de T . Existem, neste caso, dois vetores próprios linearmente independentes?
Provar que se λ é valor próprio de T, então λ n é valor próprio de T n . Generalizando, se p(t) é um polinômio então p ( λ ) é valor próprio de p(T), onde p T =a 0 1+ a 1 T+ . . .+a n T n se p ( t )=a