P2 de Cálculo 1 da UFRJ - 2020.2

Considere a função . Assinale a única alternativa verdadeira.

A função tem valor máximo local e também tem valor mínimo local.

A função tem valor mínimo local, mas não tem valor máximo local.

A função não tem nem valor máximo local nem valor mínimo local.

A função tem valor máximo local, mas não tem valor mínimo local.

A função tem infinitos valores máximos locais e também infinitos valores mínimos locais.

A derivada da função é dada por

Considere as funções e . Sabendo que e são funções deriváveis em seus domínios, a função composta tem derivada dada por:

O conjunto de todos os números críticos da função é

.

.

.

.

.

Se , então o valor de no ponto onde é

Seja uma função tal que . Então podemos afirmar que:

para todo .

.

Existe tal que .

para todo .

.

Considere a função . Então satisfaz a equação

Considere o ponto deslocando-se sobre o gráfico

, para ,

Onde e são medidos em centímetros. Denotemos por o ponto dado pela interseção do eixo com a reta tangente ao gráfico de no ponto . Sabendo que a coordenada do ponto varia a uma taxa constante de , determine com que taxa estará variando a coordenada do ponto no instante em que as coordenadas do ponto forem .

Na figura abaixo, o segmento mede e é tangente à circunferência de raio no ponto . O ponto é determinado pela interseção da circunferência com o segmento . O ponto inicia um movimento de descida, pela vertical, em direção ao ponto a uma taxa constante de .

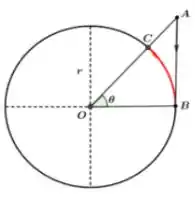
A taxa com que se movimenta o ponto , ao longo do arco , depois de segundos do ponto ter iniciado o seu movimento é

:

:

:

:

:

Dada a função , considere as afirmações:

não é ponto de mínimo local nem ponto de máximo local de .

é ponto de máximo local de .

é ponto de mínimo local de .

não possui nem mínimo nem máximo locais.

Selecione a opção correta:

A afirmação é verdadeira e as demais são falsas.

A afirmação é verdadeira e as demais são falsas.

A afirmação é verdadeira e as demais são falsas.

As quatro afirmações são falsas.

As afirmações e são verdadeiras e as demais são falsas.

Seja uma função que satisfaz a equação , qualquer que seja . Então, a equação da reta tangente ao gráfico de no ponto é

A derivada de é

.

.

.

.

.

Se , então é igual a

A equação

não tem raízes reais.

tem pelo menos três raízes reais.

: tem exatamente uma raiz real negativa, mas não tem uma raiz real positiva.

tem exatamente uma raiz real positiva, mas não tem uma raiz real negativa.

tem exatamente duas raízes reais.

Seja , onde e é uma função derivável em . Sabendo que e podemos concluir que é igual a

.

.

.

.

.

Seja uma função sobre a qual sabe-se apenas que é duas vezes diferenciável e

Considere as seguintes afirmações:

necessariamente é um valor de mínimo local.

necessariamente é um valor de mínimo global.

necessariamente é um ponto de inflexão.

necessariamente é um valor de mínimo local.

As afirmações e são verdadeiras

As afirmações e são verdadeiras

As afirmações e são verdadeiras

A afirmação é verdadeira

A afirmação é verdadeira

Dada a função , considere as afirmações abaixo:

é decrescente no intervalo ;

é côncava para baixo em

possui um máximo local em .

Podemos concluir que

As três afirmações são verdadeiras

As afirmações e são verdadeiras e a afirmação falsa.

As afirmações e são verdadeiras e a afirmação falsa.

A afirmação é verdadeira e as afirmações e falsa.

As três afirmações são falsas.

Considere as afirmações a seguir

Seja uma função diferencial em tal que e . Então existe tal que ;

Seja uma função diferencial em e suponha que existe tal que . Então ;

Sejam e funções diferenciáveis em tais que para todo e suponha, além disso, que . Então .

Podemos concluir com certeza que:

: Todas as afirmações são verdadeiras.

: Apenas a afirmação é verdadeira.

: Apenas as afirmações e são verdadeiras.

: Apenas as afirmações e são verdadeiras.

: Apenas as afirmações e são verdadeiras.