Considere o ponto deslocando-se sobre o gráfico
, para ,
Onde e são medidos em centímetros. Denotemos por o ponto dado pela interseção do eixo com a reta tangente ao gráfico de no ponto . Sabendo que a coordenada do ponto varia a uma taxa constante de , determine com que taxa estará variando a coordenada do ponto no instante em que as coordenadas do ponto forem .
Passo 1
Vem comigo que a gente resolve essa juntos!
Temos um problema de taxas relacionadas em mãos. Temos um ponto que se desloca no gráfico de e temos uma reta tangente ao gráfico dessa função que sempre vai tangenciar em e essa reta cruza o eixo em um ponto .
Então a derivada da função fornece a inclinação dessa reta tangente em .
Como anda sobre o gráfico de as suas coordenadas são obtidas a partir de então a taxa com que a coordenada de varia é a mesma para o da função .
Um fato que vai nos ajudar aqui é saber que a tangente do ângulo formado pela reta tangente ao gráfico e uma reta horizontal que passa por é igual a derivada de , já que essa derivada fornece a inclinação da reta.
Só que esse ângulo começa a contar no sentido anti-horário, e esse ângulo que mencionei acima é o seguinte:
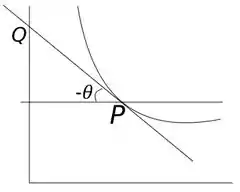
Mãos à obra então!
Passo 2
Vamos primeiro calcular a derivada de , temos que:
E isso é igual a tangente de , assim:
Passo 3
Agora levando em conta que é o ângulo formado pela reta tangente e uma reta horizontal que passa por , temos que:
Só que esse é a altura em que a reta tangente encosta no eixo , logo essa altura vai ser igual a menos a altura de e é a coordenada do ponto , assim:
Passo 4
Igualando a derivada com o termo da tangente, temos:
Mas o que queremos é a taxa temporal com que varia, então temos que derivar essa expressão em relação ao tempo, assim:
O enunciado já nos deu o valor de e queremos quando está no ponto , assim:
Logo a alternativa correta é a letra .