Na figura abaixo, o segmento mede e é tangente à circunferência de raio no ponto . O ponto é determinado pela interseção da circunferência com o segmento . O ponto inicia um movimento de descida, pela vertical, em direção ao ponto a uma taxa constante de .
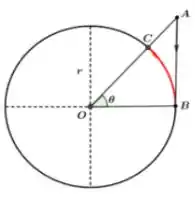
A taxa com que se movimenta o ponto , ao longo do arco , depois de segundos do ponto ter iniciado o seu movimento é
:
:
:
:
:
Passo 1
Vem comigo que a gente vai detonar essa juntos!
Temos em mãos um problema que envolve taxas relacionadas. Ele quer saber a taxa com que o ponto se move na circunferência quando depois de que começou a andar, então o que ele quer a taxa com que o ângulo muda com o tempo.
Vamos chamar de a distância entre e em um certo instante de tempo , então temos que achar uma forma de relacionar e .
Olhando a figura vemos que os pontos e são vértices de um triângulo retângulo, então:
Onde é o raio da circunferência. Assim:
Agora a gente pode derivar os dois lados da expressão que encontramos pois assim teremos uma relação entre , que é a taxa com que se move que o enunciado deu, e que é a taxa com que o ângulo muda e o que queremos saber.
Passo 2
Então temos que:
Usando que a derivada da tangente é secante ao quadrado, temos:
Usando o fato de que:
Temos:
Nós já conhecemos temos que saber quem é .
Passo 3
Vamos encontrar o , para isso vamos usar a trigonometria ao nosso favor. Cosseno de um ângulo qualquer é dado pelo cateto adjacente sobre a hipotenusa do triângulo.
O cateto adjacente no nosso caso vai ser igual ao raio da circunferência e a para achar a hipotenusa teremos que usar o teorema de Pitágoras ao nosso favor, assim:
Onde nesse caso é a distância original entre e () menos o quanto o ponto andou em .
Como o ponto anda com uma velocidade de , então em ele percorreu uma distância de , logo temos que .
Assim:
Então temos que:
Passo 4
Usando o que encontramos para , temos:
Usando que , assim:
Então a alternativa correta é letra .
Resposta
: