Exame de Proeficiência de Pré-Cálculo da UFSC - 2017.1
Pré-Cálculo - UFSC
- Sobre a equação
Pode-se afirmar que:
- não possui solução real
- possui única solução real;
- possui duas soluções reais;
- possui três soluções reais;
- possui infinitas soluções reais.
- Sobre a equação
Pode-se afirmar que:
- Não possui solução real;
- Possui única solução real;
- Possui duas soluções reais;
- Possui três soluções reais;
- Possui infinitas soluções reais.
Qual é o número de soluções da equação
No intervalo de ?
- Nenhuma solução
- Uma solução
- Duas soluções
- Três soluções
- Quatro soluções
- Considere a função dada por
Podemos afirmar que:
- é periódica de período fundamental ;
- é periódica de período fundamental ;
- é periódica de período fundamental ;
- é periódica e o período fundamental pertence a ;
- não é periódica.
18. Seja dada por
Se e , então é igual a
- ;
- ;
- ;
- Nenhuma das respostas anteriores.
19. Sobre a equação
Pode-se afirmar que:
- não possui solução em ;
- possui única solução em
- possui duas soluções em
- possui três soluções em
- possui quatro soluções em
- Seja um número real e considere a função dada por
O maior valor de para o qual é uma função injetiva é
- ;
- ;
- ;
- .
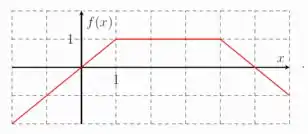
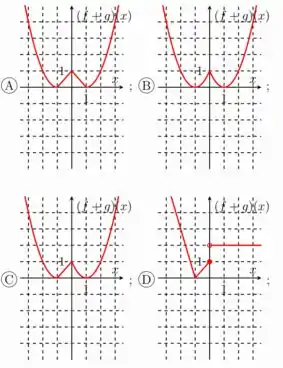
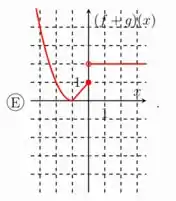
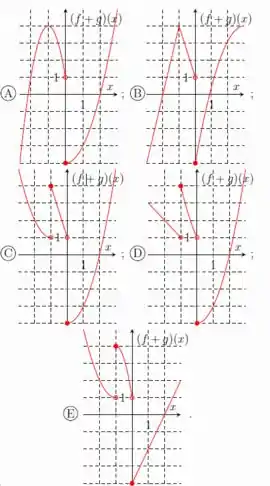
- Considere as funções e definidas por
E
O gráfico que melhor representa a função é
- Considere as sentenças
- a composta de duas funções ímpares é uma função ímpar;
- a composta de uma função ímpar e uma função par é uma função par, independente da ordem;
- a composta de duas funções pares é uma função par.
Pode-se afirmar que:
- somente (I) e (II) são verdadeiras;
- somente (I) e (III) são verdadeiras;
- somente (II) e (III) são verdadeiras;
- somente (III) é verdadeira;
- todas as afirmações são verdadeiras.