Listas Pré Cálculo de Pré-Cálculo da UFSC - Lista 11
Pré-Cálculo - UFSC
Na hora de fazer o gráfico de uma função, qual é a vantagem de se saber previamente se uma função é par ou ímpar?
Ver solução completaDiga quais das funções abaixo são injetoras, sobrejetoras ou bijetoras, considerando ℝ como contra-domínio para todas elas.
Sejam uma função e um intervalo contido no domínio de . Dizemos que é crescente em se para quaisquer e com . Em outras palavras, o valor de aumenta à medida que aumenta. Similarmente dizemos que é decrescente em se para quaisquer e com . Quando dizemos que é crescente (sem mencionar intervalo), significa que é crescente em todo seu domínio (o mesmo se aplica para decrescente). Por exemplo, considere a função cujo gráfico é dado pela figura abaixo.
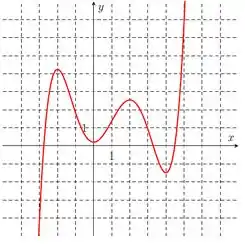
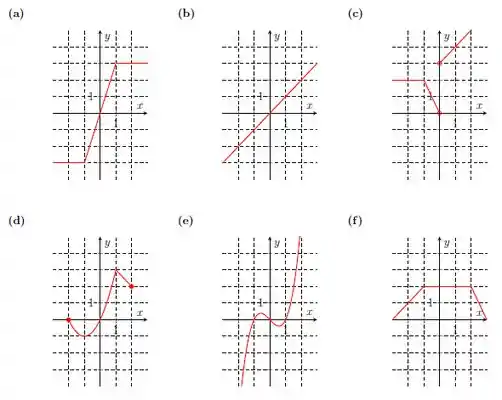
Note que a função é crescente em , em e em e é decrescente em e em . Nos itens abaixo, diga os intervalos de crescimento e decrescimento das funções.
Considere a função cujo gráfico está no enunciado do exercício anterior. Observe que, próximo ao ponto , todos os valores de são menores ou iguais a . Nesse caso, dizemos que é um máximo local para . Da mesma forma, também é um máximo local. Com um raciocínio análogo, dizemos que e são mínimos locais. Outra forma de expressar é dizer que possui máximos locais em e e mínimos locais em e . Nos itens abaixo, determine os máximos e mínimos locais, assim como os valores de nos quais são atingidos.
Seja uma função com domínio simétrico em relação à origem (por exemplo, um domínio da forma ). Dizemos que é uma função par se para todos . Se para todos , dizemos que é uma função ímpar. Por exemplo, é uma função par, pois para todo , . A função é uma função ímpar, pois para todo , . A função não é nem par nem ímpar, pois e essa expressão não é igual a para todo . O gráfico das funções pares possui a propriedade de ser simétrico em relação ao eixo das ordenadas (isto é, a metade esquerda e a metade direita do gráfico são espelhadas). O gráfico das funções ímpares possui a propriedade de ser simétrico em relação à origem (isto é, se o ponto pertence ao gráfico , então o ponto também pertence). Complete o gráfico da função em que uma parte do gráfico está desenhada abaixo, sabendo que:
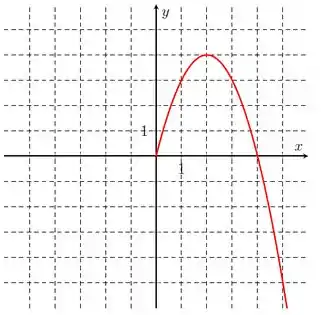
a) A função é par
b) A função é ímpar
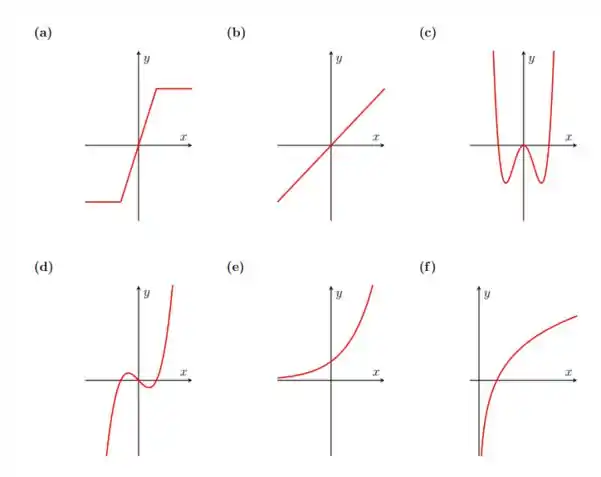
Ver solução completaDetermine quais funções são pares, quais são ímpares ou nehuma nem outra.
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaDetermine quais das funções abaixo são injetoras. Se a resposta for positiva, determine o conjunto imagem e encontra a função inversa (para isso, considere o contradomínio igual à imagem).
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaTodas as funções abaixo são injetoras (verifique!). Encontre a inversa dessas funções (assumindo contradomínio igual ao conjunto imagem).
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
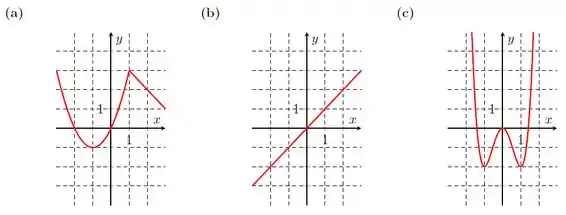
Ver solução completaNos itens abaixo, faça o gráfico da inversa da função cujo gráfico está representado.
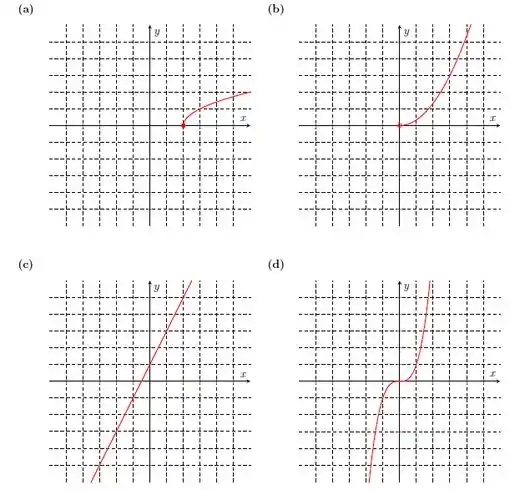
Seja uma função inversível (isto é, que possui inversa) e suponha que e que . Determine e .
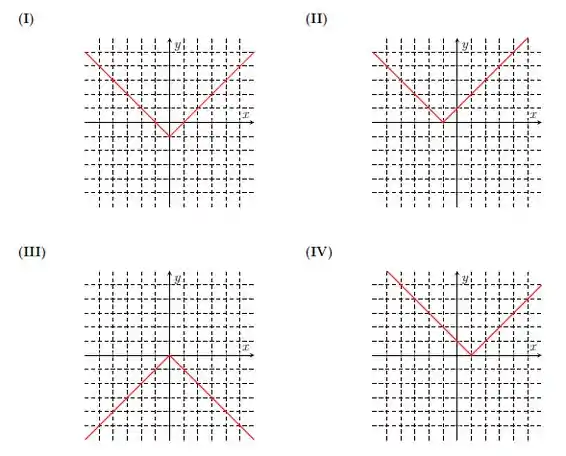
Ver solução completaSuponha que seja conhecido o gráfico de uma função . Em cada item, descreva como obter o gráfico da função a partir do gráfico da função .
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
n)
o)
p)
q)
r)
s)
t)
Ver solução completaNos itens abaixo, explique como obter o gráfico da função a partir do gráfico da função .
a) e
b) e
c) e
d) e
e) e
f) e
Ver solução completaUse o gráfico da função para desenhar o gráfico das funções abaixo.
a)
b)
c)
d)
Ver solução completaFaça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
.
Ver solução completaFaça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
.
Ver solução completaFaça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
Ver solução completaFaça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
Ver solução completaEm cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
; o gráfico é transladado unidades para cima.
; o gráfico é transladado unidade para baixo.
; o gráfico é transladado unidades para a esquerda.
; o gráfico é transladado unidade para a direita.
Ver solução completaEm cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
o gráfico é transladado unidades para a direita e para cima.
o gráfico é refletido em relação ao eixo e transladado unidade para cima.
o gráfico é transladado unidades para a esquerda e refletido em relação ao eixo .
Ver solução completaEm cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
o gráfico é esticado verticalmente por um fator , transladado unidades para baixo e para a direita.
o gráfico é encolhido verticalmente por um fator , transladado uma unidade para a esquerda e para cima.
o gráfico é refletido em relação à reta
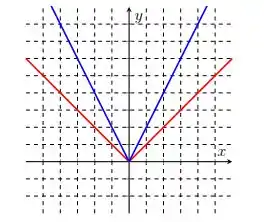
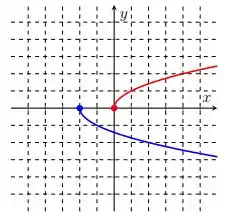
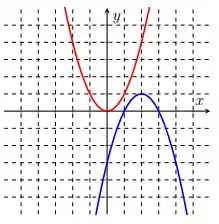
Ver solução completaNos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
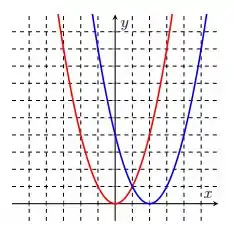
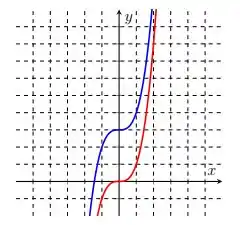
Nos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
.
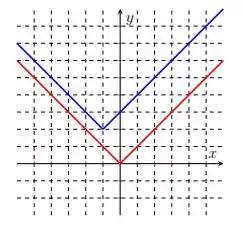
.