UFSC – Pré-Cálculo – Exame de Proficiência 2017.1
- Considere as funções e definidas por
E
O gráfico que melhor representa a função é
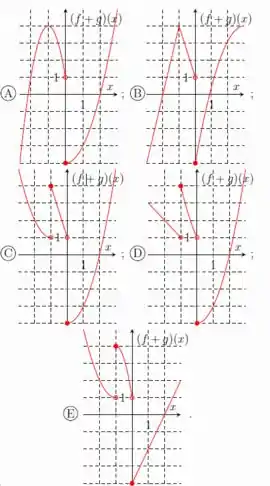
Passo 1
Fala aí pessoal! Nos deparamos com um problema de gráficos de funções. Como temos a forma das duas funções
E
Nossa tarefa é construir a função a partir dessas informações e ver como que é o comportamento do gráfico dessa nova função em cada um dos intervalos. Vamos começar fazendo essa soma!
Passo 2
Para somar essas funções que são definidas em intervalos, a gente tem que somar as contribuições das funções no mesmo intervalo... como assim? Olha lá, se olhar a primeira parte de temos que ele é quando o é menor que zero. Então a gente soma em cada parte de que tenha :
A última parte a gente ainda não sabe. Arrumando essas expressões, temos
Passo 3
Agora a gente tem que ver o comportamento da função nos outros intervalos. Como para . Somamos em cada termo de nesse intervalo. Assim ó:
Arrumando isso aí, temos a expressão completa da nossa função:
Agora só nos resta olhar o comportamento do gráfico de cada parte dessa função.
Passo 4
Para temos
Isso é uma reta com inclinação negativa. Como não temos , o que daria
ela deve ser aberta neste ponto. Beleza??Para temos
Essa função é uma parábola voltada para cima. Podemos pegar o seu valor nos extremos do intervalo para ter uma noção do seu comportamento:
Não podemos esquecer que é aberta em , naquele ali!
Passo 5
Para temos
Outra parábola voltada para cima!! No extremo temos
E já sabemos que ela cresce a partir deste ponto com o formato parabólico!Só para reunir tudo, temos que ter um gráfico que começa com uma reta de inclinação negativa até o ponto e é aberta neste ponto. A partir daí temos uma parábola de concavidade para cima que começa em e vai até o ponto e é aberta neste ponto também. Por fim, temos outra parábola de concavidade para cima que começa no e cresce sem parar...Com isso, o gráfico tem que ser:
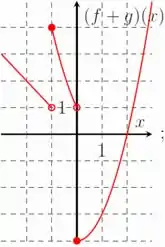
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
Letra D.