UFSC – Pré-Cálculo – Exame de Proficiência 2017.1
- Considere a função dada por
Podemos afirmar que:
- é periódica de período fundamental ;
- é periódica de período fundamental ;
- é periódica de período fundamental ;
- é periódica e o período fundamental pertence a ;
- não é periódica.
Passo 1
Fala aí pessoal! Olha, o problema tá pedindo para a gente ver a periodicidade da função
Bom gente, uma função período é aquela que se repete depois de um período . Pensando no gráfico a gente tem que o desenho dela sempre se repete quando a gente anda unidades em . Beleza? Então a gente precisa ou ver se existe um tal que
Ou pensar no gráfico dessa função e ver se existe algum padrão. Eu prefiro esse caminho aqui para funções trigonométricas então vamos lá!!
Passo 2
A gente sabe que a função é uma função periódica. Ela sempre tem resultados entre e dessa forma aqui:
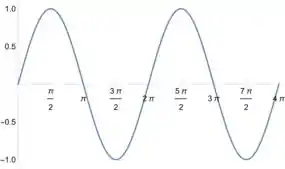
A onde a gente percebe que essa função é periódica com período . Beleza... mas não é isso que a gente tem, nós temos essa função ao quadrado. Bom, olhando a função a gente já consegue ter uma ideia.
Aquelas partes que estão para baixo são valores negativos da função. Quando elevadas ao quadrado vão ficar positivas, ou seja, é como se a gente espelhasse aquela montanha ali. Só que elas vão ser exatamente iguais às partes que já eram positivas... No fundo vamos ter algo como essa função aqui:
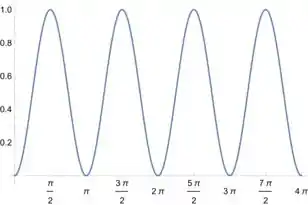
Onde a gente percebe que ela se recebe sempre quando andamos . Ou seja, ela é periódica com período dado por !
E resolvemos esse problema 😊 Vamos para a próxima?
Resposta
Letra c.