UFSC – Pré-Cálculo – Exame de Proficiência 2017.1
- Seja um número real e considere a função dada por
O maior valor de para o qual é uma função injetiva é
- ;
- ;
- ;
- .
Passo 1
Fala aí pessoal! Nos deparamos com um problema em que ele nos dá uma função
que é uma parábola voltada para cima, nos dá um domínio e nos pede para achar o maior valor de para que seja injetiva. Bom, para lembrar, uma função injetiva é aquela em que a gente nunca vai ter dois valores de com o mesmo valor de ... Bem, como temos uma parábola voltada para cima, sabemos que ela vem diminuindo (para valores pequenos de ) passa pelo vértice e começa a subir de maneira espelhada em relação ao vértice. Assim ó:
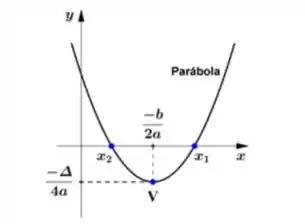
A gente percebe então que a partir do vértice passamos a ter dois com um mesmo valor de e isso é o que a gente não quer!O que a gente vai fazer então é encontrar esse vértice e parar o domínio nele mesmo, ou seja, o do problema é o do vértice! Partiu?
Passo 2
A nossa função é dada por
Sempre que temos uma função do segundo grau (botei umas linhas para a gente não se confundir com as letras do problema dado, ok?), o do vértice é dado por
Em nossa função temos e , então
Como discutimos antes, esse é o valor máximo de do domínio dado que a função pode ser injetiva, ou seja:
E aí resolvemos essa questão 😊 Vamos para a próxima?
Resposta
Letra A.