Listas Pré Cálculo de Pré-Cálculo da UFSC - Lista 10
Pré-Cálculo - UFSC
14. Para as funções do item anterior, determine os pontos do eixo das abscissas e do eixo das ordenadas que pertencem ao gráfico.
Ver solução completa15. Encontre uma equação para a reta que passa pelos pontos abaixo.
(a) e .
(b) e
Ver solução completa16. Determine uma equação para a reta que passa pelo ponto e tem coeficiente angular igual a .
Ver solução completa17. Faça o gráfico e encontre o conjunto imagem das funções abaixo. Identifique os pontos em que o gráfico intersecta os eixos coordenados e os pontos nos quais há uma mudança no comportamento do gráfico (por exemplo, um vértice de uma parábola).
e)
f) .
Ver solução completa17. Faça o gráfico e encontre o conjunto imagem das funções abaixo. Identifique os pontos em que o gráfico intersecta os eixos coordenados e os pontos nos quais há uma mudança no comportamento do gráfico (por exemplo, um vértice de uma parábola).
c)
b) .
Ver solução completa17. Faça o gráfico e encontre o conjunto imagem das funções abaixo. Identifique os pontos em que o gráfico intersecta os eixos coordenados e os pontos nos quais há uma mudança no comportamento do gráfico (por exemplo, um vértice de uma parábola).
a)
b) .
Ver solução completa20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
a)
Ver solução completa20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
c)
Ver solução completa20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
b)
Ver solução completa21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
a) e .
Ver solução completa21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
b) e .
Ver solução completa21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
c) e .
Ver solução completa23. Considere as funções e cujos gráficos estão representados abaixo. Calcule o que se pede (se fizer sentido):
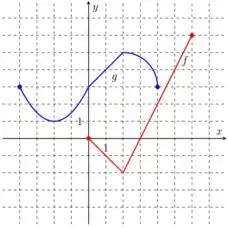
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
(f) ;
(g) ;
(h) .
Ver solução completa22. Considere as funções e . Calcule o que se pede:
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
(f) ;
(g) ;
(h) .
Ver solução completaSejam e conjuntos. Defina o que é uma função de em . Como são chamados os conjuntos e ? Defina conjunto imagem.
Ver solução completaDiga quais das tabelas abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
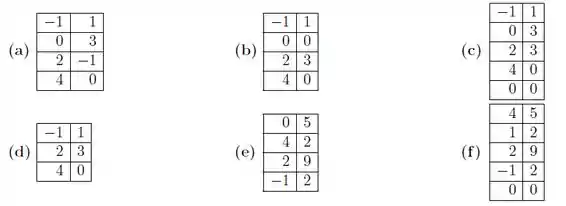
Diga quais dos conjuntos abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
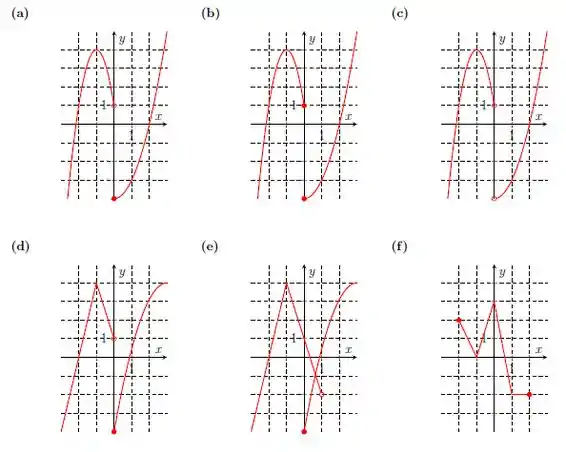
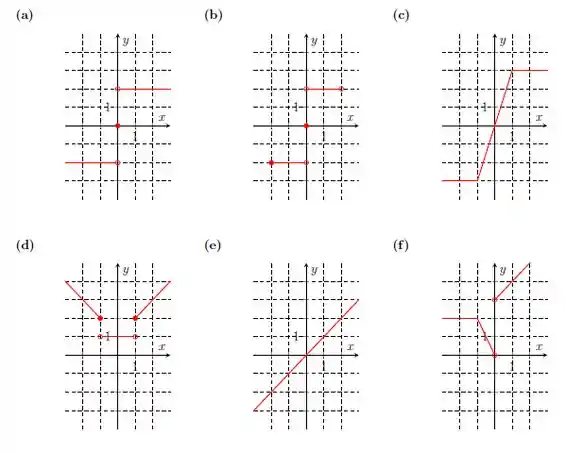
Ver solução completaDiga quais dos gráficos abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
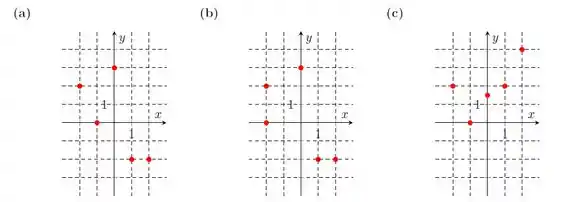
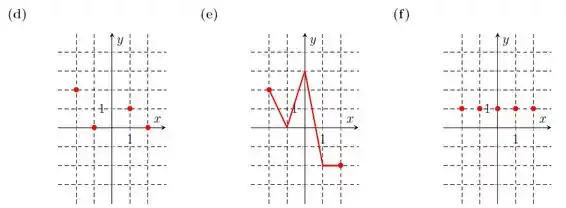
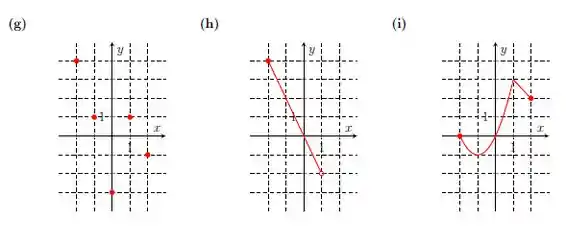
Diga quais dos gráficos abaixo representam alguma função. Nos casos que são funções, determine o domínio.
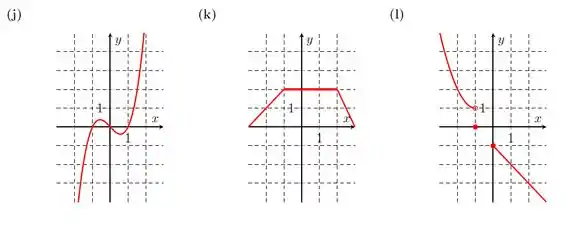
Os gráficos abaixo representam funções. Determine o domínio e a imagem de cada uma delas.
Em cada um dos itens abaixo calcule o que se pede.
a) dada por . Calcule .
b) dada por . Calcule .
Ver solução completaAo criar uma função (ou definir uma função, usando o linguajar matemático), devemos especificar o domínio, o contradomínio e a regra de formação (ou regra de associação) da função. Por exemplo, dada por tem domínio , contradomínio e regra de formação . Porém, nem sempre essas três informações fornecem uma função. Por exemplo dada por não é uma função, pois a regra não pode ser aplicada a todos os elementos do domínio. Neste
caso, dizemos que não está bem definida (caso fosse uma função, diríamos que está bem definida).
Em cada um dos itens abaixo, diga quais estão ou não bem definidos.
a) dada por
b) dada por
c) dada por
d) dada por
e) dada por
f) dada por é o número cujo quadrado é .
Ver solução completaSempre que uma função não está bem definida (conforme exercício anterior), podemos fazer certas alterações para a tornar bem definida. Há, basicamente, três formas de fazer isso: (A) restringir o domínio, (B) aumentar o contradomínio ou (C) modificar a regra de formação. Para cada um dos itens do exercício anterior que não estão bem definidos, corrija a definição utilizando um dos três métodos acima, conforma no exemplo do item (a).
Ver solução completaNormalmente, o caminho para se definir uma função é escolher o domínio, o contradomínio e, por fim, a regra de formação. Porém, em certas situações, a regra de formação é escolhida inicialmente. Nesse caso, fica a pergunta de que escolhas podemos fazer para o domínio e o contradomínio de forma que se obtenha uma função bem definida. Por exemplo, para a regra de formação podemos escolher como domínio e como contradomínio. Obviamente, há infinitas escolhas que funcionam nesse caso. Convencionou-se, nos cursos de Cálculo que, quando uma regra de formação é fornecida (sem domínio e contradomínio), o domínio é o maior subconjunto de de forma que a regra de formação possa ser calculada dentro do conjunto dos números reais e que o resultado também seja um número real. Por exemplo, o maior subconjunto de para o qual a expressão pode ser calculada usando número reais é . Com isso, dizemos que o domínio da função é . Em cada um dos itens abaixo, encontre o domínio das funções, conforme exemplos nos itens (a) e (b).
Observação. Não há uma convenção absoluta para o contradomínio quando este não é especificado. As duas convenções mais usadas são usar ou usar o conjunto imagem como contradomínio.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaFaça o gráfico das funções abaixo, encontrando alguns dos pontos pertencentes ao gráfico e tentando deduzir o restante. O objetivo aqui é mostrar que existe uma forma de fazer o gráfico de qualquer função, basta encontrarmos diversos pontos pertencentes ao seu gráfico. Obviamente, esse método é entediante, mas é importante utilizá-lo uma vez na vida. Ao longo desse curso, aprenderemos técnicas para encontrar o gráfico de certas funções sem precisar recorrer ao método desse exercício. Futuramente, em Cálculo , você aprenderá mais técnicas para traçar o gráfico de funções.
a) dada por
b) dada por
c) dada por
d) dada por
Ver solução completaFaça o gráfico das funções abaixo (a partir daqui, você pode usar seus conhecimentos sobre funções para fazer o gráfico):
a)
b)
Ver solução completa