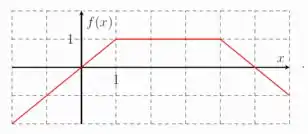
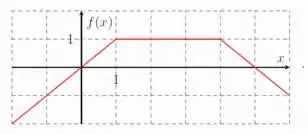
- Seja a função definida pelo gráfico
A lei que define é
Passo 1
Fala aí pessoal! Nos deparamos com um probleminha para a gente encontrar a lei de uma função a partir desse gráfico aqui
Encontrar a lei é encontrar a expressão que define essa função em vermelho que apareceu para a gente. Vamos primeiro entender o comportamento dela e daí a gente parte para resolver esse problema. Bom, a primeira coisa que a gente percebe é que a nossa função tem 3 intervalos:
- Ela começa como uma reta de inclinação positiva (algo com a cara , com ) até o ;
- Daí ela vira uma função constante de até ;
- Por fim, ela se torna uma reta com inclinação negativa (algo com a cara , com ) e continua assim até o final.
Com isso em mente já dá para eliminar algumas alternativas né? Só dá para ser ou a letra c. ou a letra e. Mas vamos lá encontrar essas funções aí!
Passo 2
Vamos começar com a primeira reta. Precisamos encontrar quem é e de:
A gente faz isso pegando dois pontos do gráfico. Vamos pegar e pois sabemos o resultado da função nesses pontos:
Da última expressão temos
Devolvendo isso na primeira, a gente encontra
Dessa maneira, para temos
Passo 3
A parte do meio é de boa. Para temos uma função constante
Passo 4
Por fim, vamos fazer a mesma coisa para descobrir a cara da última reta. Precisamos encontrar quem é e de:
A gente faz isso pegando dois pontos do gráfico. Vamos pegar e pois sabemos o resultado da função nesses pontos:
As duas expressões nos dão o sistema
Fazendo a primeira expressão menos a segunda temos
Devolvendo o valor de na primeira expressão temos
Opa! Com isso a gente tem a expressão da função para :
Passo 5
Juntando os nossos resultados temos
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
Letra C.