UFRJ, Álgebra Linear, P3 – 2017.2, Questão 05
Calcule a distância do ponto ao plano
(a)
(b)
(c
(d)
Passo 1
Precisamos achar a reta que é perpendicular ao plano e contém o ponto Assim, vamos achar o ponto e calcular que vai ser a própria distância :
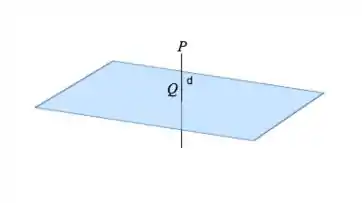
Passo 2
O vetor diretor da reta que queremos vai ser aquele cujas coordenadas são os coeficientes das variáveis da equação do plano,
A equação paramétrica da reta vai ser então:
Queremos achar o ponto interseção dela e do plano, então vamos achar a equação cartesiana para poder fazer o sistema linear:
Substituindo nas outras equações, temos:
Juntando com a equação do plano, temos um sistema:
Resolvendo isso aí, temos que
Passo 3
Agora é só calcular
Resposta
a
Exercícios de Livros Relacionados
Seja T um isomorfismo de um espaço vetorial V. Provar que se u , v é um produto interno sobre V, então o mesmo acontece com a função P T : V × V → R definida por P T ( u , v ) = T ( u ) , T ( v ) .
Sejam f ( t )=a 0 + a 1 t + a 2 t ² + . . . + a n t n e ² g ( t )=b 0 + b 1 t + b 2 t ² + . . . + b n t n ² polinômios quaisquer de P n ( R ) . A função ( f ( t ) , g ( t ) ) →a 0b 0 + a 1 b 1 + . . .
Seja V = R 4 munido do produto interno usual, determinar um vetor não nulo v ∈ R 4 que seja ortogonal a v 1 = ( 1 ,1 ,1 ,- 1 ) , v 2 = ( 1 ,2 ,0 ,1 ) e v 3 = ( - 4 ,1 ,5 ,2 ) .
No espaço V = P 2 consideremos o produto interno f t ∙ g t =∫ 0 1 f t ∙ g td t . Calcular f t ∙ g t e | f t | para f t = t 2 - 2 t e g t = t + 3 .
Consideremos no R 3 , o seguinte produto interno: x 1 , y 1 , z 1 ∙ x 2 , y 2 , z 2 = 2 x 1 x 2 + y 1 y 2 + 4 z 1 z 2 Determinar, em relação a esse produto interno, um vetor unitário simultaneamente o