Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Norma de um Vetor e Distância entre dois Vetores

Ver Teoria
Exercício 261234567891011121314151617181920212223242527

Enunciado

PUCRIO, G1-2019.1

  1. Considere o segmento de reta C onde A = ( 3 ,   3 ) e B = 8 ,   6 . Determine os vértices de C e D do retângulo cuja diagonal é A B - e seus lados são paralelos aos eixos coordenados. Determine a área do retângulo.
  2. Considere a ,   b ,   c , x ,   y ∈ R diferentes de 0 e os pontos do plano R 2 .

    3. P x ,   y ,     Q a + x ,   b + y ,     R x - b c ,   y + a c

    Prove que estes pontos determinam um triângulo retângulo e determine seus catetos.

  3. Considere os vetores u = 0 ,   1 ,   - 1 e w = ( 2 ,   k ,   0 ) , onde k ∈ R . Determine todos os possíveis valores de k de modo que os vetores u e u + w sejam perpendiculares.
  4. Considere um vetor u de R 3 tal que u = 5 . Seja v um etor de R 3 tal que o vetor u + v ≠ 0 → é perpendicular (ortogonal) ao vetor u - v ≠ 0 → . Determine v .

Passo 1

Show de bolinhas galera, na letra (a) o enunciado deu pra gente o ponto A = ( 3 ,   3 ) e o ponto B = 8 ,   6 , e além disso ele diz pra gente que o segmento A B - é a diagonal de um retângulo. E pede pra gente determinar os outros dois vértices C e D do retângulo. Belezoca, se a gente colocar esses pontos no plano, vamos ter:

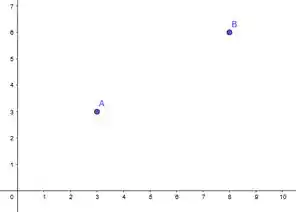
E o segmento A B - é a reta que liga esses dois pontos:

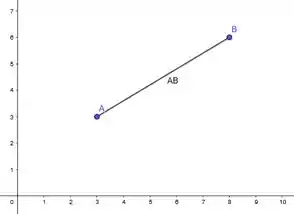
Logo, essa é a diagonal do retângulo. E como o enunciado garante pra gente que os lados do retângulo são paralelos aos eixos, temos que eles cruzam as respectivas linhas:

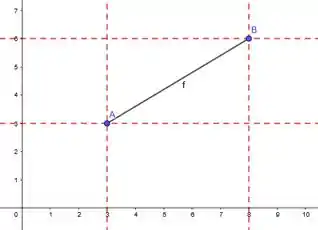
Portanto, os vértices C e D são justamente onde essas linhas pontilhadas se cruzam:

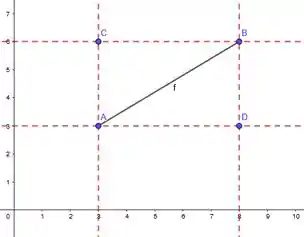
Dados por C = ( 3 ,   6 ) e D = 8 ,   3 . E dessa forma podemos também medir seus lados pra podermos calcular a área. A base b do retângulo mede:

b = 8 - 3 = 5

E a altura h :

h = 6 - 3 = 3

Logo a área do retângulo é:

A = 5 × 3 = 15

Passo 2

Belejóia então galera, continuando na letra (b), o enunciado forneceu pra gente que 3 pontos no plano R 2   :

P x ,   y ,     Q a + x ,   b + y ,     R x - b c ,   y + a c

Ele afirma ainda que a ,   b ,   c , x ,   y ∈ R e são diferentes de 0 . Não contente com isso, ele pede pra gente provar que esses pontos forma um triângulo retângulo!

Mas peraí, vamos com carinho. Um triângulo retângulo é aquele que possui um ângulo reto em um de seus vértices. Então se a gente conseguir provar que existem dois segmentos perpendiculares entre si, formado por esses pontos, então sim, teremos um triângulo retângulo. Os segmentos que que podemos formar com esses pontos são:

P Q - = Q - P = a + x ,   b + y - x ,   y = a ,   b

R P - = P - R = x ,   y - x - b c ,   y + a c = b c ,   - a c

R Q - = Q - R = a + x ,   b + y - x - b c ,   y + a c = a + b c ,   b - a c

Então temos um total de 3 segmentos, que são os 3 lados do triângulo. Se dois desses lados formarem um ângulo reto, então teremos que esse triângulo é retângulo. E pra gente poder testar isso, podemos usar as relações de produto interno, já que quando fazemos o produto interno entre dois vetores perpendiculares/ortogonais o resultado é 0 , ou seja, dados dois vetores quaisquer u e v , se:

u ,   v = 0

Então u e v são ortogonais.

Então partiu testar o produto interno com os segmentos que a gente encontrou:

P Q - ,   R Q - = a ,   b ,   a + b c ,   b - a c = a a + b c + b b - a c

P Q - ,   R Q - = a 2 + a b c + b 2 - a b c = a 2 + b ²

E não deu igual a 0 , logo pra esses dois segmentos, não temos perpendicularidade. Agora testando com o R P - , temos:

P Q - ,   R P - = a ,   b ,   b c ,   - a c = a b c + b - a c = a b c - a b c = 0

E olha o danado aí, se o nosso produto interno entre P Q - e   R P - resultou em 0 , quer dizer que esses dois segmentos são ortogonais, e além disso, ELES SÃO OS CATETOS! Portanto formam um ângulo reto!! E já que o ponto P se repete nos dois segmentos, quer dizer que o ângulo reto é em P .

E só pra garantir, vamos testar o produto interno para os outros segmentos também:

R Q - ,   R P - = a + b c , �� b - a c ,   b c ,   - a c = b c a + b c - a c b - a c

R Q - ,   R P - = a b c + b 2 c 2 - a b c + a 2 c 2 = c 2 a 2 + b 2

Que também é diferente de 0 . Portanto os pontos:

P x ,   y ,     Q a + x ,   b + y ,     R x - b c ,   y + a c

Formam sim um triângulo retângulo! Os catetos são P Q - e   R P - :

P Q - = a ,   b

R P - = b c ,   - a c

Passo 3

Agora na letra (c), o enunciado deu pra gente os vetores u = 0 ,   1 ,   - 1 e w = ( 2 ,   k ,   0 ) , onde k ∈ R . E pede pra gente determinar todos os valores possíveis de k de modo que os vetores u e u + w sejam perpendiculares.

Calma aí, porque a gente sabe que para dois vetores serem perpendiculares, o produto interno entre eles deve ser 0 . Iradoso, então podemos encontrar o vetor u + w e ver quanto vale o produto interno dele com u :

u + w = 0 ,   1 ,   - 1 + 2 ,   k ,   0

u + w = 2 ,   k + 1 ,   - 1

Logo, o produto interno entre u e u + w fica assim:

u , u + w = 0 ,   1 ,   - 1 , 2 ,   k + 1 ,   - 1

u , u + w = 0 2 + k + 1 + 1

u , u + w = k + 2

E como queremos que eles sejam perpendiculares, o resultado desse produto interno tem que ser 0 , logo:

u , u + w = 0

k + 2 = 0

k = - 2

Portanto, para k = - 2 , os vetores u e u + w são perpendiculares.

Passo 4

E por fim na letra (d), o enunciado deu pra gente que existe um vetor u de R 3   tal que u = 5 , e além disso também existe um vetor v de R 3 tal que u + v ≠ 0 → é perpendicular (ortogonal) ao vetor u - v ≠ 0 → . Belezoca, depois que ele falou tudo isso, ele pediu pra gente calcular v .

Chuchu beleza então galera, se os vetores u - v e u + v são ortogonais, quer dizer que o produto interno entre eles é 0 , isto é:

u - v , u + v = 0

E é aqui que a malandragem fez morada, porque agora podemos “distribuir” esse produto interno, saca só.

Primeiro para u - v :

u - v , u + v = u , u + v - v , u + v = 0

E agora abrindo u + v , temos:

u , u + v - v , u + v = u , u + u , v - v , u - v , v = 0

E como u , v = v , u , temos que:

u , u - v , v = 0

u , u = v , v

E como o módulo de um vetor é calculado através da fórmula:

u = u , u

E temos que u = 5 , chegamos que:

u , u = 5

E para v temos:

v = v , v

u , u = v , v

v = u , u

E por fim, descobrimos que o módulo de v era igual ao módulo de u

v = u

v = 5

Resposta

  1. A = 15
  2. Os catetos são: P Q - = a ,   b e R P - = b c ,   - a c .
  3. k = - 2 .
  4. v = 5 .

Exercícios de Livros Relacionados

Seja T um isomorfismo de um espaço vetorial V. Provar que se u , v é um produto interno sobre V, então o mesmo acontece com a função P T : V × V → R definida por P T ( u , v ) = T ( u ) , T ( v ) .
Sejam f ( t )=a 0 + a 1 t + a 2 t ² + . . . + a n t n e ² g ( t )=b 0 + b 1 t + b 2 t ² + . . . + b n t n ² polinômios quaisquer de P n ( R ) . A função ( f ( t ) , g ( t ) ) →a 0b 0 + a 1 b 1 + . . .
Seja V = R 4 munido do produto interno usual, determinar um vetor não nulo v ∈ R 4 que seja ortogonal a v 1 = ( 1 ,1 ,1 ,- 1 ) , v 2 = ( 1 ,2 ,0 ,1 ) e v 3 = ( - 4 ,1 ,5 ,2 ) .
No espaço V = P 2 consideremos o produto interno f t ∙ g t =∫ 0 1 f t ∙ g td t . Calcular f t ∙ g t e | f t | para f t = t 2 - 2 t e g t = t + 3 .
Consideremos no R 3 , o seguinte produto interno: x 1 , y 1 , z 1 ∙ x 2 , y 2 , z 2 = 2 x 1 x 2 + y 1 y 2 + 4 z 1 z 2 Determinar, em relação a esse produto interno, um vetor unitário simultaneamente o