Mostre que os gráficos das funções e se cruzam em algum ponto no intervalo . Sugestão: Utilize o Teorema do Valor Intermediário
Passo 1
Fala povo bonito, tudo certo? Olha só, vamos lá. Quando duas funções se cruzam elas geram um ponto em comum, certo? Mesmo e mesmo ! Então é bem seguro de afirmar que:
Em algum ponto. Ok, mas como isso ajuda a gente? Olha só a doidera, se eu fizer essa manipulação:
Definido , o problema muda de cara! O enunciado poderia ser muito bem reescrito para:

E a gente agora vai partir exatamente desse enunciado reescrito, beleza?
Passo 2
A questão ainda é boazinha com a gente e nos dá uma dica. Pelo TVI, temos válido que:

Em grafiquês, é como se a gente tentasse ligar esses pontos:
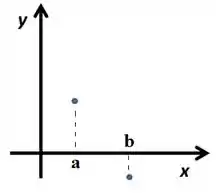
Ou esses pontos:
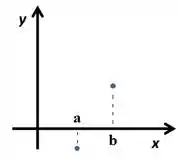
De forma contínua, sem passar pelo eixo , o que não é possível! Como não dá pra fazer isso, garantimos a existência de pelo menos uma raiz nesse intervalo.
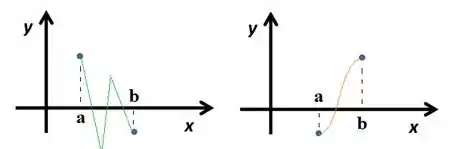
Passo 3
Ok, sem mais delongas, vamos ver a nossa questão em específico, onde:
No intervalo que o enunciado dá, temos o seguinte valor pra essa função:
Opa, caímos então nesse caso:
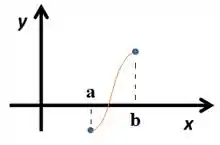
E pelo Teorema do Valor Intermediário, tá prova então que tem raiz em , o que, por extensão, prova que em algum lugar dentro do intervalo
Resposta
Desenvolvimento acima