Seja C o conjunto das funções diferenciáveis tao que:
Considere o subconjunto de definido por:
Sejam m e M os elementos mínimo e máximo de , respectivamente. O valor de 2M-7m é
Passo 1
Opa galera aqui é uma questão, que a uma primeira visão é totalmente abstrata e não da para tirar muita informação. Ou seja, normalmente a uma primeira visão estamos totalmente perdidos, né assim que pensamos?

MAS CAAAAAAAAAALMINHA, não precisa se preocupar vamos lembrar de analisar todas as informações da questão.
Em síntese o que a questão quer? Precisamos encontrar os valores de máximos e mínimos dessa função. Normalmente precisamos de uma expressão para derivar e achar os pontos críticos e olhando qaí não temos nada disso né?
Mas olha de novo, nos temos os valores das derivadas dentro de um intervalo. Então essa informação já possuímos.

Mas e o resto? Bem, temos apenas valores então nossa única saída é utilizar o teorema do valor médio e encontrar estimativas desses pontos de máximo e mínimos através dele. Então vamos lá?
Ahhhhhhhhh lembrando o teorema do valor médio corresponde a seguinte informação
Geometricamente a derivada é o coeficiente angular da reta tangente, o TVM nos informa que podemos calcular a derivada em um único ponto através da secante da curva, graficamente estamos fazendo a seguinte operação:
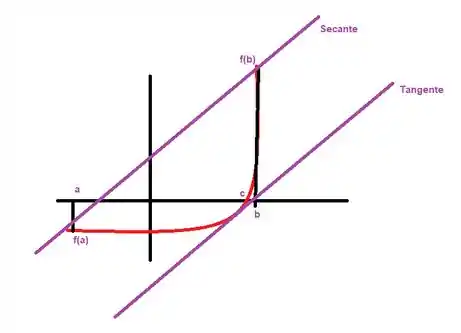
Iae conseguiu enxergar que a reta tangente é paralela a secante nesse caso? Então vamos utilizar o teorema do valor médio para calcular em qual ponto é possível realizar isso nesse caso.
Agora podemos ir lá?
Passo 2
Para um primeiro momento vamos aplicar o teorema do valor médio nos nossos dados, com isso temos a seguinte igualdade
Agora vamos analisar o que acontece com a variação da minha função nos extremos do meu domínio.
Primeiramente vamos admitir que ao fazer isso estamos analisando o limite superior, logo temos que:
Logo como estamos no extremo superior temos que qualquer valor dentro da função deve ser menor do que ele, logo:
Realizando a mesma análise para o limite inferior temos que:
Gerando a seguinte igualdade:
Logo temos os maiores e menores valores possíveis da função sendo assim:
Ahhh e só para deixar mais claro o porque disso é valido é que uma função bem comportada ao longo de um domínio fechado existe um teorema que fala que existe pelo menos um máximo ou mínimo.
Passo 3
Resultando em
Resposta
A Resposta final é a letra