O número de soluções reais da equação é:
- 0
- 1
- 2
- 6
Passo 1
Bem, para resolvermos essa e outras questões que te pedir para analisar quantas raízes tem uma equação, e você não souber resolver a equação analiticamente como uma do segundo grau, por exemplo, vou te introduzir uma ideia muito bacana! Veja só:
Quero te indagar o seguinte:
Qual a única chance de termos uma única raiz em uma função? Olha a imagem e tenta me responder:
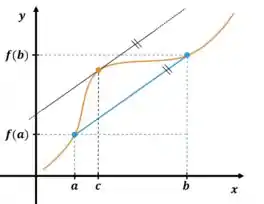
Veja bem que a função é sempre crescente, então não tem como dela ter mais de uma raiz! Mas ela pode ter uma ou nenhuma sem problemas, saca?
Isso acontece, pois para ela ser sempre crescente a primeira deriva deve...
Mas ela também poderia ser apenas decrescente e o raciocínio é o mesmo, ou seja nesse caso a primeira deriva seria sempre
Passo 2
Agora, tenta me responder essa daqui oh:
Qual a única chance de termos duas únicas raizes em uma função? Olha a imagem e tenta me responder:
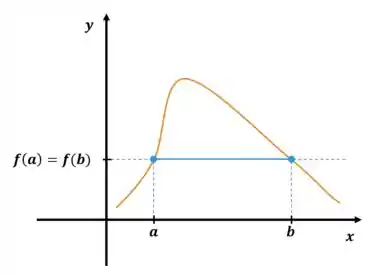
Isso acontece só acontece se a concavidade for só pra baixo ou só pra cima. Em matematiquês a segunda derivada, que nos fala sobre a concavidade, deve ser apenas...
Passo 3
Perceba então que para mais raízes o raciocínio é sempre o mesmo, ou seja, para termos até três raízes deve rolar para todo no domínio que:
Para termos até quatro raízes deve rolar para todo no domínio que:
Sacou?
Passo 4
Agora, depois dessa aulinha, estamos preparados para voltar ao nosso problema:
Se chamarmos o lado esquerdo de ...
Podemos derivar a vontade:
Veja que ainda fica difícil de dizer alguma coisa, pois não sabemos se a função cúbica dai é sempre positiva ou sempre negativa... Então derivemos mais uma vez...
HAHA! Veja que essa derivada só é positiva, afinal de contas se chamarmos
E tentarmos calcular o zero dessa equação do segundo grau:
O delta dá negativo significando que não tem raiz! Como o termo que multiplica é positivo, então a função é inteiramente positiva:
Isso nos mostra que a nossa função pode ter até duas raiz reais apenas!
Passo 5
Eliminando a alternativa e , as demais continuam na jogada, afinal a função ainda pode assumir raizes, ou , o que ela não pode ter é mais que isso saca?
Vamos então usar agora o Teorema do Valor Intermediário, lembra dele? Não? Calma, não precisa rir de nervoso que agora você não esquece mais:
Basicamente, esse teorema afirma que se uma função é continua em um intervalo fechado e muda de sinal dentro dele, obrigatoriamente existe uma raíz da função nesse intervalo. Então, pra sabermos quantas raízes a função tem, precisamos achar intervalos em que ela muda de sinal.
Passo 6
Observe que
e
Logo, no intervalo existe uma raíz. Além disso, note que
Portanto, no intervalo também há uma raíz.
Veja que encontramos dois intervalos onde tem uma raiz, logo a equação tem duas raízes. Como vimos, ela não pode ter mais já que
Então a resposta correta é...