Seja uma função contínua em ℝ tal que e , e seja . A função composta possui duas raízes negativas distintas. Determine intervalos abertos disjuntos contendo cada uma dessas raízes.
Passo 1
Bom, a questão pede os intervalos contendo as raízes, isso nos dá um indício de que vamos usar o teorema do valor intermediário. Vamos ter:
Só nos resta partir das únicas informações que temos disponíveis:
Ou seja, estes pontos no gráfico cartesiano são assim:
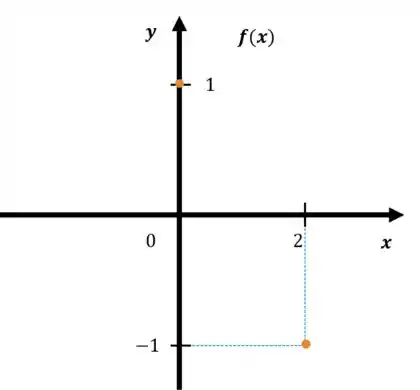
O teorema do valor intermediário diz que se uma função é contínua, como essa nossa é, ela vai ter um valor para a função entre e em algum lugar entre e .
Isto significa que a função troca de sinal entre e já que é positivo e é negativo, assim precisa ter o entre eles dois como diz o teorema do valor intermediário.
Isso significa que a função troca de sinal entre e .
Passo 2
Igualando, podemos descobrir quais valores de fazem ser igual a 0 e 2:
Resolvendo a equação de segundo grau, as soluções de estão no conjunto abaixo:
Isso resulta nos seguintes pontos de
Isso porque fizemos
Então o valor de nesses pontos é
Analogamente, as soluções de estão no conjunto abaixo:
Isso resulta nos seguintes pontos de
Isso porque fizemos
Então o valor de nesses pontos é
No gráfico cartesiano de , teríamos o seguinte:
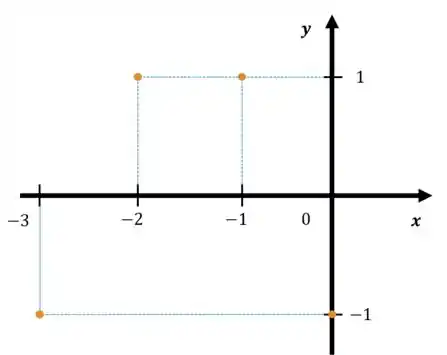
Passo 3
Portanto, como podemos ver, a função troca de sinal no intervalo:
E também no intervalo:
E pelo teorema do Valor Intermediário, temos que existe ao menos uma raiz em cada um desses intervalos, conforme queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)