Exercícios de Teorema do Valor Intermediário e Funções Monótonas - Lista de Exercícios Resolvida
Questão 3
Seja uma função contínua em ℝ tal que e , e seja . A função composta possui duas raízes negativas distintas. Determine intervalos abertos disjuntos contendo cada uma dessas raízes.
Ver solução completaQuestão 4
2) Considere as funções e . Prove que os gráficos de e se intersectam em um único ponto quando .
Ver solução completaQuestão 5
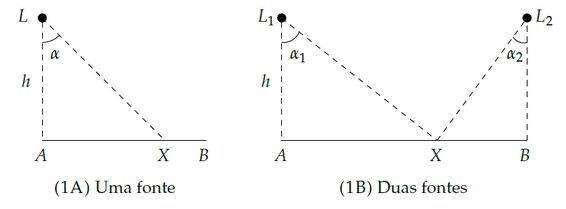
2) Sejam uma fonte luminosa puntiforme de potência e um segmento de reta que dista de (vide Figura ). A intensidade luminosa em , que dista de , é dado por:
Onde é uma constante. Considere agora, conforme a Figura , duas fontes e (com potências e e respectivamente) emitindo luz sobre os pontos de um segmento de comprimento . Mostre que existe um único ponto em sobre o qual a intensidade luminosa é máxima.
Questão 6
Use o teorema do valor intermediário para mostrar que a equação
Possui pelo menos uma solução real.
Ver solução completaQuestão 7
A equação
tem exatamente uma raiz real positiva, mas não tem uma raiz real negativa.
tem pelo menos três raízes reais.
: não tem raízes reais.
tem exatamente duas raízes reais.
tem exatamente uma raiz real negativa, mas não tem uma raiz real positiva.
Ver solução completaQuestão 9
b) Determine o valor ou valores de tal que do Teorema do Valor Médio, onde no intervalo .
Ver solução completaQuestão 11
Prove que a equação admite uma única raiz real. Determine um intervalo de amplitude que contenha tal raiz.
Ver solução completaQuestão 14
Use o teorema do valor intermediário (TVI) para mostrar que a equação
Tem uma solução no intervalo . Relemebre que
Ver solução completaQuestão 15
Seja C o conjunto das funções diferenciáveis tao que:
Considere o subconjunto de definido por:
Sejam m e M os elementos mínimo e máximo de , respectivamente. O valor de 2M-7m é
Ver solução completaQuestão 16
Verifique se as funções definidas a seguir são monótonas em todo o seu dom��nio. Em caso afirmativo, mostre matematicamente de qual tipo ela é (crescente, decrescente, não-crescente ou não decrescente). Em caso negativo, justifique o porquê dela não o ser. Represente, em cada caso, o gráfico da função no plano cartesiano.
tal que .
Ver solução completaQuestão 17
Verifique se as funções definidas a seguir são monótonas em todo o seu domínio. Em caso afirmativo, mostre matematicamente de qual tipo ela é (crescente, decrescente, não-crescente ou não decrescente). Em caso negativo, justifique o porquê dela não o ser. Represente, em cada caso, o gráfico da função no plano cartesiano.
tal que
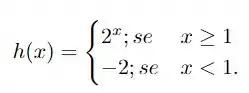
Questão 18
Verifique se as funções definidas a seguir são monótonas em todo o seu domínio. Em caso afirmativo, mostre matematicamente de qual tipo ela é (crescente, decrescente, não-crescente ou não decrescente). Em caso negativo, justifique o porquê dela não o ser. Represente, em cada caso, o gráfico da função no plano cartesiano.
tal que
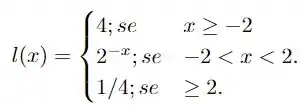
Questão 19
Verifique se as funções definidas a seguir são monótonas em todo o seu domínio. Em caso afirmativo, mostre matematicamente de qual tipo ela é (crescente, decrescente, não-crescente ou não decrescente). Em caso negativo, justifique o porquê dela não o ser. Represente, em cada caso, o gráfico da função no plano cartesiano.
tal que .
Ver solução completaQuestão 20
Seja . Mostre que tem exatamente uma raiz real e localize-a entre dois inteiros consecutivos.
Ver solução completaQuestão 21
Seja .
Quantas raízes reais distintas tem a equação ?
Mostre que a equação tem exatamente três raízes reais distintas.
Ver solução completaQuestão 22
Mostre que os gráficos das funções e se cruzam em algum ponto no intervalo . Sugestão: Utilize o Teorema do Valor Intermediário
Ver solução completaQuestão 23
Mostre que os gráficos das funções e se cruzam em algum ponto no intervalo . Sugestão: Utilize o Teorema do Valor Intermediário
Ver solução completaQuestão 24
Resolva os itens abaixo justificando detalhadamente suas soluções.
Use o Teorema do Valor Intermediário para mostrar que o gráfico de
tem um ponto horizontal no intervalo (ponto horizontal é onde a tangente é horizontal).
Ver solução completa