UFSCAR, Sem Campus, Cálculo 1, Listas Cálculo 1 - UFSCAR - Tarefa 3 - Fundamentos de Probabilidade, Questão 1d
Verifique se as funções definidas a seguir são monótonas em todo o seu domínio. Em caso afirmativo, mostre matematicamente de qual tipo ela é (crescente, decrescente, não-crescente ou não decrescente). Em caso negativo, justifique o porquê dela não o ser. Represente, em cada caso, o gráfico da função no plano cartesiano.
tal que
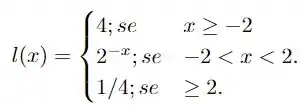
Passo 1
Eaew, tudo bem?
Nós temos que determinar em cada alternativa desta questão se a nossa função é monótona (ou não), e tendo esta informação determinar se a função é crescente, decrescente, não-crescente ou não-decrescente. Mas o que são estas coisas?
Uma função monótona pode ser resumida como uma função que é sem não-crescente (não-decrescente), ou seja, sua derivada nunca muda de sinal para diferentes valores de no domínio. A função nesta alternativa é
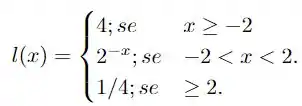
Ao longo dos passos iremos revisar o que define a função como crescente (decrescente) e assim por diante! Vamos lá!
Passo 2
Mesmo definida em intervalos, nossa função é contínua (você pode verificar fazendo os limites laterais em e ). Temos dois intervalos em que a função é constante, isso já elimina que ela seja crescente ou decrescente, pois existem momentos em que nenhum dos dois acontece! Mas ela ainda pode ser não-decrescente ou não-crescente! Vamos verificar o intervalo intermediário, beleza?
Para valores de negativos, como o domínio são os inteiros, temos apenas , a função vale , para positivos, temos apenas , em que a função vale . O único valor do domínio entre esses valores é , e a função vale . Ou seja, a função é monotônica e não-crescente!
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
A função é monotônica e não-crescente!