Unicamp, Cálculo 1, 2019.2, P1, Questão 4.
Use o teorema do valor intermediário (TVI) para mostrar que a equação
Tem uma solução no intervalo . Relemebre que
Passo 1
Então pessoal, vamos começar revisando o que o teorema do valor intermediário diz pra gente.
Vamos supor que você tenha uma função contínua num intervalo que vai de até no eixo e de até no eixo .
Algo parecido com isso aqui:
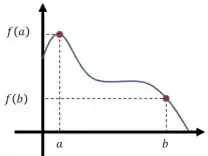
Aí o teorema te diz o seguinte. Se você me disser algum valor que está entre e , então é garantido que em algum momento entre e , a função vai assumir esse valor.
Por exemplo, você me diz que está entre e . Então eu posso ter certeza que existe algum ponto entre e que satisfaz:
Passo 2
Beleza, como a gente pode usar isso pra provar que a equação tem uma solução entre e ?
Bom, vamos começar olhando a igualdade:
A solução dessa equação acontece quando essa função aqui:
É igual a zero!
Então a gente tem que provar que existe algum ponto entre e em que . Percebeu a semelhança com o que foi dito lá na nossa explicação do TVI?
Passo 3
Já que a função é contínua, a gente quer provar que o zero fica entre e .
Se isso acontece, então é garantido pelo TVI que existe algum ponto entre e que satisfaz .
Ou seja, existe algum ponto nesse intervalo que é solução da equação.
Então vamos calcular :
E :
Lembrando que , dá pra aproximar esse resultado:
Beleza! Isso satisfaz a condição que a gente queria:
Dá uma olhada no gráfico:
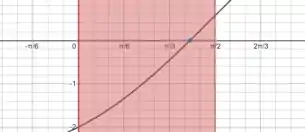
Então existe solução no intervalo que foi dado!
Resposta
Demonstração.